A simple circuit
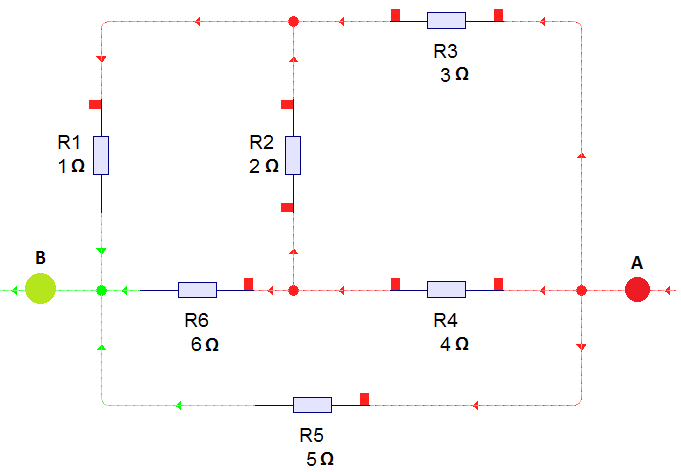
If the equivalent resistance between points and of the circuit above is in ohms, find .
The answer is 1742.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we convert the R 2 - R 4 - R 6 star connection to a delta connection ( Y- Δ transform ) as shown in the figure above. Then the three delta equivalent resistors are:
R 2 4 R 4 6 R 6 2 = R 6 R 2 R 4 + R 4 R 6 + R 6 R 2 = 6 2 × 4 + 4 × 6 + 6 × 2 = 6 4 4 = 3 2 2 Ω = 2 4 4 = 2 2 Ω = 4 4 4 = 1 1 Ω
From the equivalent circuit, we have:
R e q = ( 1 ∣ ∣ 1 1 + 3 ∣ ∣ 3 2 2 ) ∣ ∣ 2 2 ∣ ∣ 5 = ( 1 2 1 1 + 3 1 6 6 ) ∣ ∣ 2 2 ∣ ∣ 5 = 3 7 2 1 1 3 3 ∣ ∣ 2 2 ∣ ∣ 5 = 1 1 3 3 3 7 2 + 2 2 1 + 5 1 1 = 1 . 7 4 2 8 0 8 7 9 9
Therefore, ⌊ 1 0 3 R e q ⌋ = 1 7 4 2