A simple geometry-circled question
In the circle below with centre , the points , , and are situated on the circle. The measure of is .
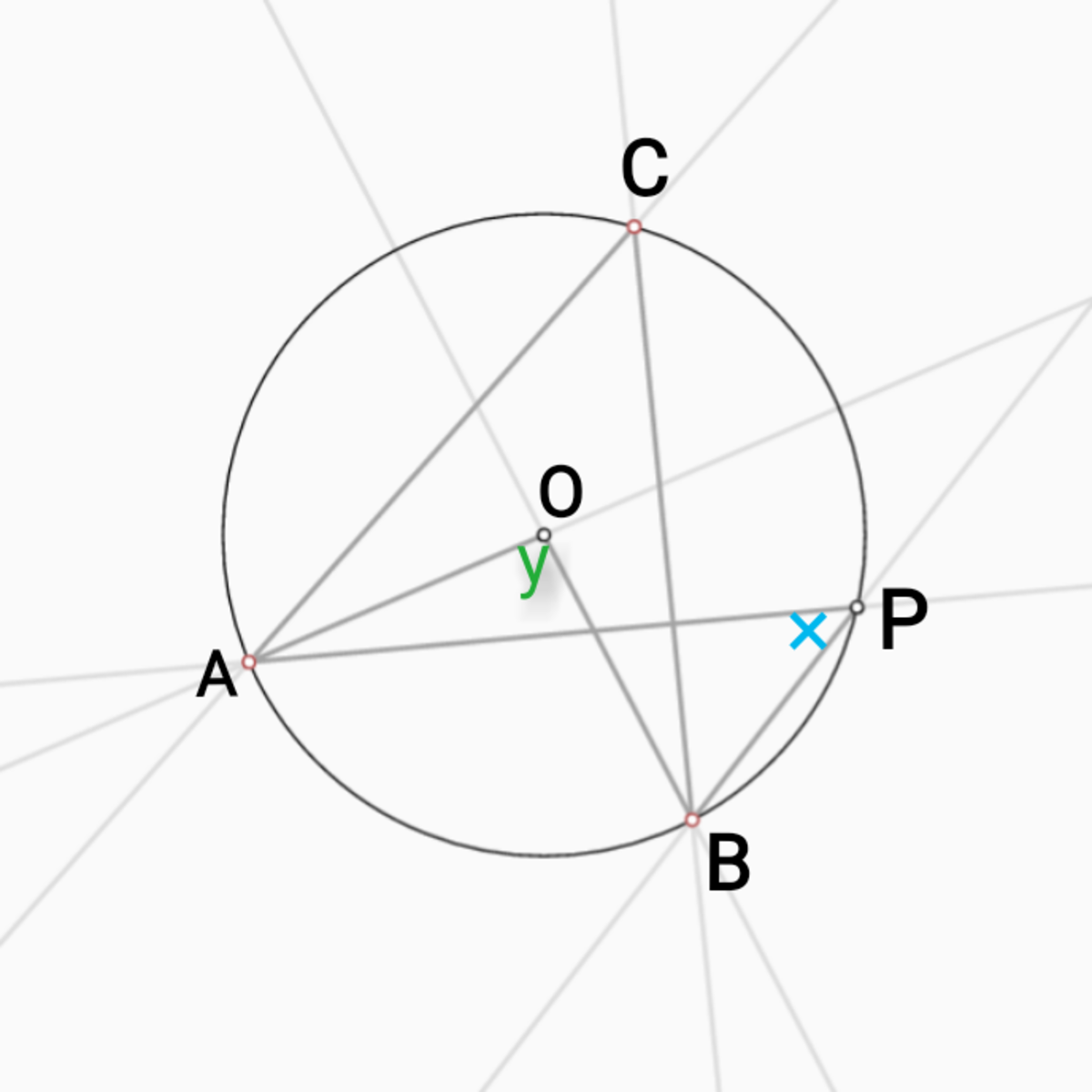
What are the values of ( ) and ( ) in degrees in the diagram?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In a circle, all inscribed angles with the same endpoint/startpoint are equivalent to each other, which shows that
As an angle with the intersection point as the centre of a circle and the end points lying on the circle are twice the angle value of an inscribed angle, we can assure that
Therefore, the correct choice for the question is choice 4