The Midpoint Chord
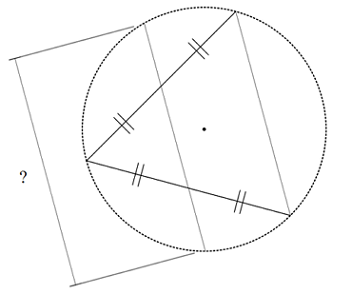
An equilateral triangle of side length 2 units is inscribed in a circle. Find the length of a chord of this circle which passes through the midpoints of two sides of the triangle.
Give your answer up to 3 decimal places.
The answer is 2.236.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Great way to calculate the length of a chord by finding the perpendicular distance to the center.
Let L , M be the midpoints of the sides of the triangle. Let X , Y be the intersection of the chord with the circle so the order of points on the chord is X L M Y .
Clearly L M = 1 because the smaller triangle is similar to equilateral triangle by S A S and 2 2 = 1
Let X L = x . By symettry, M Y = x . By intersecting chords at M , X M × M Y = 1 × 1 . As M is a midpoint of the triangle.
X M × M Y = 1 ⇒ ( x + 1 ) ( x ) = 1 ⇒ x 2 + x − 1 = 0 ⇒ x = 2 − 1 + 5 as x > 0 .
So X Y = 2 × 2 − 1 + 5 + 1 = − 1 + 5 + 1 = 5
So the answer is 5 = 2 . 2 3 6
Moderator note:
Nice usage of power of a point to figure out the length of this segment.
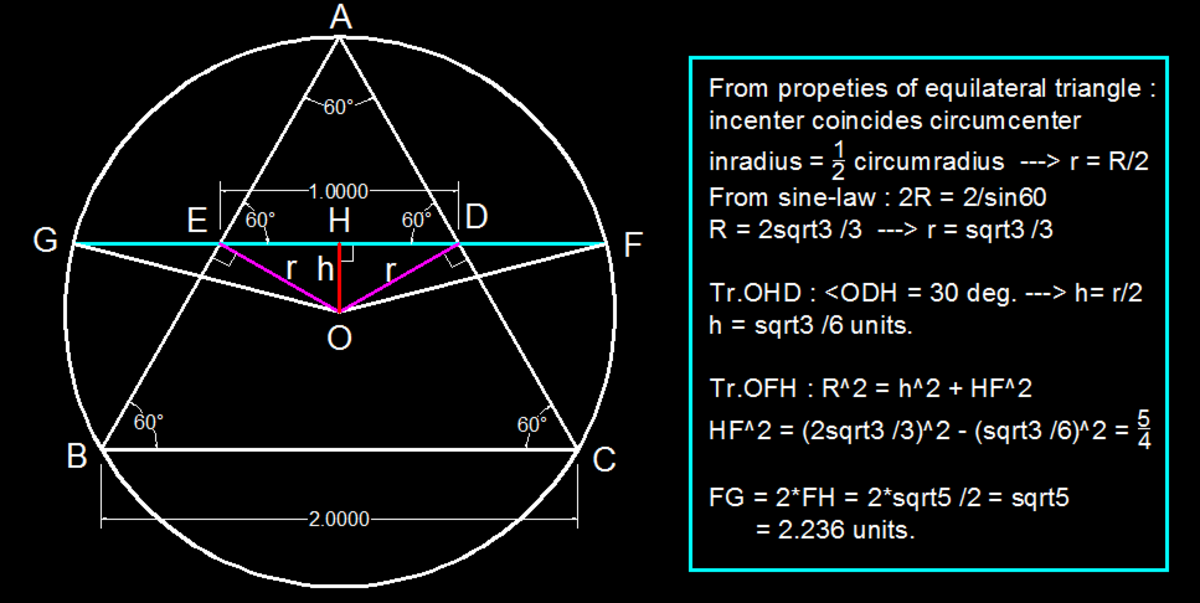
B a s e d o n t h e p r o p e r t i e s o f e q u i l a t e r a l t r i a n g l e . T h e a l t i t u d e o f t h e t r i a n g l e = 2 C o s 3 0 = 3 , ∴ c i r c u m r a d i u s , R = 3 2 ∗ 3 a n d c h o r d a l s o p a s s t h r o u g h m i d p o i n t o f t h e a l t i t u d e . ⟹ d i s t a n c e o f t h e c h o r d f r o m c e n t e r , d = 3 2 ∗ 3 − 2 3 = 2 ∗ 3 1 C h o r d l e n g t h = 2 ∗ R 2 − d 2 = 5 = 2 . 2 3 6 .