A Simple Polygon
A simple polygon with 2018 sides is drawn starting from a vertex P inside a square. None of its vertices is on a side of the square and none of the vertices of the square is on a side of the polygon. Among the following options, what number can be the number of intersections between the sides of the square and the sides of the polygon?
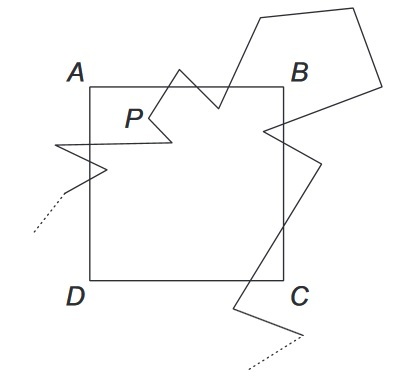
Problem From OBMEP (Brazilian Math Olympiads) 2018
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The number has to be even - as both figures are simple polygons, so if one intersection has the square going out, there has to be next which has it going in.
The number cannot be more than 4036 - as a straight line, and there are only 2018 of them, can only intersect the square two times.
The only possible answer that qualifies is 8 1 6 .