Too Many Numbers To Be Added!
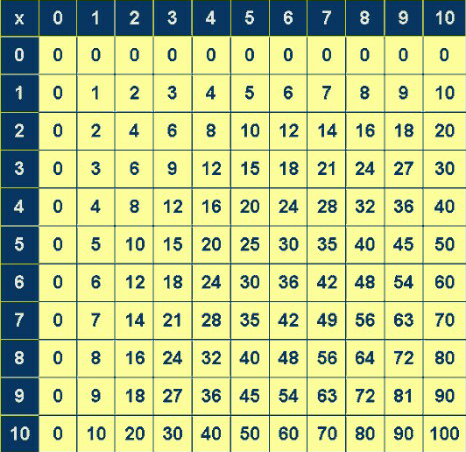
What is the sum of all number in the yellow square in the above multiplication table?
The answer is 3025.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
I did a mistake and got the question wrong but my method was just fine. I noticed the increment of 55 so I did ((550+55)/2)*10 to find my answer.
Ignore the Zeros. On the first row we have 1+2+3+4+5+6+7+8+9+10=55= X On the second row we have 2X, third row 3X..... Sem it all you have 55X = 3025
This is also how i did it.
We observe that in each row, the sum of the numbers are n = 0 ∑ 1 0 n x where x is the corresponding number in the 1 s t column. For example in in row 2 , the sum of numbers is n = 0 ∑ 1 0 2 n .
So, we have to evaluate
n
=
0
∑
1
0
n
+
2
n
+
3
n
+
⋯
+
9
n
+
1
0
n
.
=
n
=
0
∑
1
0
(
2
1
0
×
1
1
)
n
=
n
=
0
∑
1
0
5
5
n
=
3
0
2
5
.
Sum of Row 0 and Row 10 is 550.
R o w 0 + R o w 1 0 = R o w 1 + R o w 9 R o w 1 + R o w 9 = R o w 2 + R o w 8 This pattern continues through the table. (0 and 10, 1 and 9, 2 and 8, 3 and 7, 4 and 6) 5 5 0 × 5 = 2 7 5 0 Sum of Row 5 is 275 2 7 5 0 + 2 7 5 = 3 0 2 5
We have 1+2+3+4+5+...+100 =1(1+2+...+10)+2(1+2+3+...+10)+3(1+2+...+10)+...9(1+2+3+...+10)+10(1+2+3+...+10) =(1+2+3+4+5+6+7+8+9+10)(1+2+3+4+5+6+7+8+9+10) =55*55=3025
Second row = 11x5 Third row = 22x5...... Till last row = 110x5 Take 5 common 5(11+22+33.....110) take 11 common =5x11(1+2+3.....10) =55(55) =3025
You've got numbers from 1 to 10 in the problem and since it's a multiplication square you end up multiplying all the different numbers which is like when you're expanding double brackets the inside and then the outside. Anyway in the end it's just the sum of 1 to 10 squared which is 55 squared which is 3025
Each column is equal to the bottom number multiplied by half the size of the column. 11 numbers in each column makes it: 5.5*(10+20+30+40+50+60+70+80+90+100)
11+110, 22+99....=121 in each pair. 5x121=605 605x5=3025
I know it's a bit blunt but it worked.
You can also do it by assuming that in each row the sum of all the numbers will be a ∗ 1 0 + 2 a ∗ 1 0 where a is a number from 1 to 10. For instance, the sum of the 10 row is 5 5 0 + 5 0 , thus you can consider using only the column a ∗ 5 sum all its numbers and multiplying the result by 10 you obtain 2 7 5 0 . At this point you have to add the value of the 5 column to find the answer to this problem 2 7 5 0 + 2 7 5 = 3 0 2 5 .
S = 5×(1+10) + 5×(2+20) + 5×(3+30) + 5×(4+40) + 5×(5+50) +....+ +... + 5×(10+100)
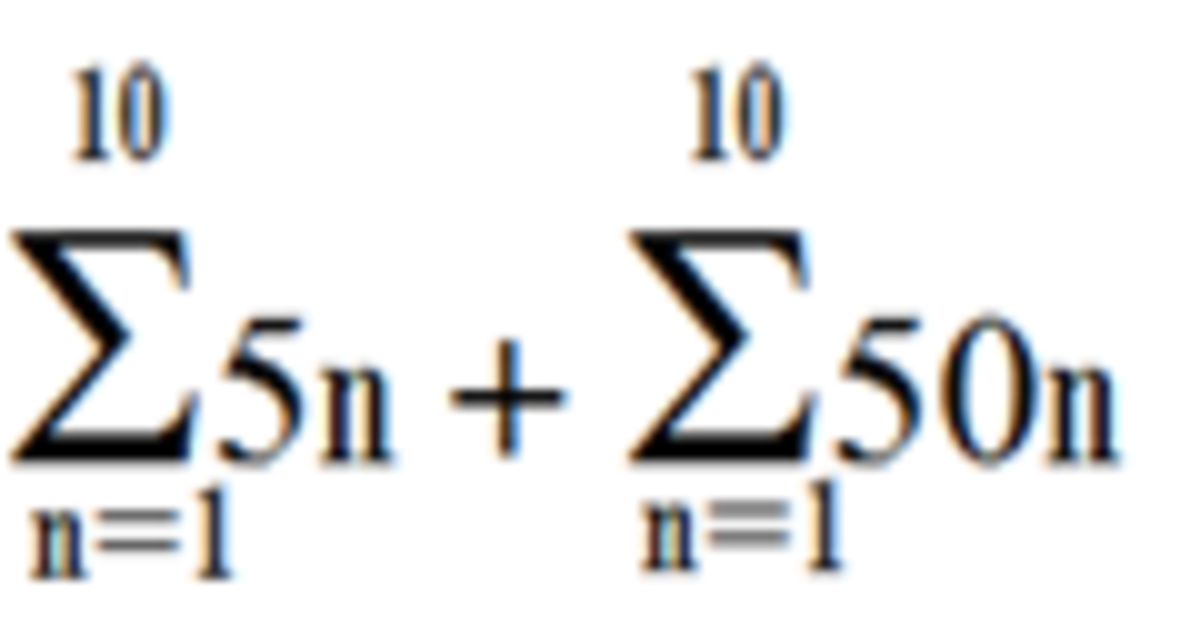
= (5 + 10 + 15 + 20 + 25 +...+ 50) + (50 +100 + 150 + 200 +...+ 500) =
= 5×(5+50) + 5×(50+500) = 25+250+250+2500
ans: 3025
v e r t i c a l ( i = 0 ∑ 1 0 i ) × h o r i z o n t a l ( i = 0 ∑ 1 0 i ) = 5 5 × 5 5 = 3 0 2 5
Note : We use the fact that 1 + 2 + 3 + ⋯ + n = 2 1 n ( n + 1 ) .