A simple triangle-semi-circle problem

Geometry Level 3

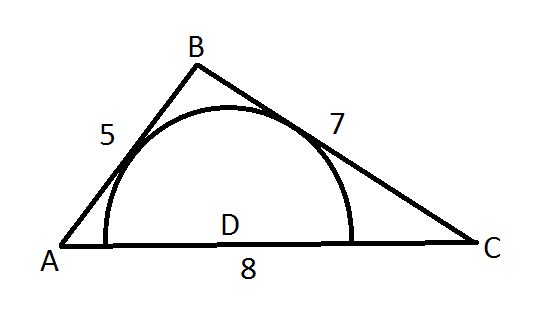
△ A B C \triangle ABC has sides of lengths 5 , 7 5, 7 and 8 8 . You draw a semi-circle on the longest side touching the 5 5 and 7 7 sides, as in the figure above. Find the radius of the semi-circle. If the radius can be written as a b \dfrac{ a } {\sqrt{b} } , where b b is square-free, then enter a + b a + b .


The answer is 8.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Hosam Hajjir
Jun 13, 2019

The area of △ A B C \triangle ABC by Heron's formula is A = s ( s − a ) ( s − b ) ( s − c ) A = \sqrt{ s (s - a) (s - b)(s - c) } , where s = ( 1 / 2 ) ( 8 + 5 + 7 ) = 10 s = (1/2) (8 + 5 + 7 ) = 10 . Thus, A = 10 ( 2 ) ( 5 ) ( 3 ) = 10 3 A = \sqrt{10 (2) (5)(3) } = 10 \sqrt{3} . A A , on the other hand, is given by A = ( 1 / 2 ) R ( 5 + 7 ) = 6 R A = (1/2) R (5 + 7 ) = 6 R , so R = 5 3 3 = 5 3 R = \dfrac{5 \sqrt{3} }{3} = \dfrac{5}{\sqrt{3} } .

2 Helpful 2 Interesting 6 Brilliant 0 Confused

Hmmmm, interesting. I'm not aware of the formula Area of a triangle = 1 2 × ( sum of 2 of the triangles’ lengths ) × ( radius of the semicircle inscribed in said triangle, tangent to both the chosen sides, and its diameter lie on the remaining side ) \text{Area of a triangle} = \frac12 \times (\text{sum of 2 of the triangles' lengths} ) \times ( \text{ radius of the semicircle inscribed in said triangle, tangent to both the chosen sides, and its diameter lie on the remaining side} )

What a mouthful!

Got a proof for it?

Pi Han Goh - 1 year, 11 months ago

The proof is very straightforward. Connect the center of the semi-circle (point D) with point B with a line segment. This line segment divides △ A B C \triangle ABC into two smaller triangles. Since the the semi-circle is tangent to AB (say at point E) and to BC (say at point F), then DE is equal to the radius in length and is perpendicular to AB, and the same can be said as DF, its length is R, and it is perpendicular to BC. Thus in △ A D B \triangle ADB the base is A B AB and the height is DE = R, and similarly in △ D B C \triangle DBC the base is BC and the height is DF = R, and this implies that

Area of △ A B C = Area of △ A D B + Area of △ D B C = 1 2 ( A B + B C ) R \text{Area of } \triangle ABC = \text{Area of } \triangle ADB + \text{Area of } \triangle DBC = \dfrac{1}{2} ( AB + BC ) R

Q . E . D . \bold {Q.E.D.}

Hosam Hajjir - 1 year, 11 months ago

Log in to reply

OH GOD I'M AN IDIOT

Pi Han Goh - 1 year, 11 months ago
Fletcher Mattox
Sep 26, 2020

Reflect the triangle about the line AC to form a tangential quadrilateral (a kite, specifically). Then solve for the radius of the inscribed circle.

inradius = K s \frac{K}{s} \hspace{1cm} as shown here

where K K is the area of the quadrilateral (twice the area of the triangle) and s s is its semiperimeter.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...