A simple triangular Problem.

Geometry Level 3

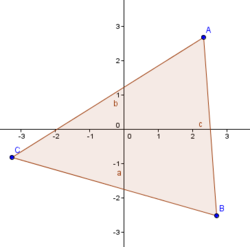Let $z_1,z_2,z_3$ be the coordinates of the vertices of $\Delta ABC$ . If $|z_1|=|z_2|=|z_3|$ and $z_1+z_2+z_3=0$ , then the triangle $ABC$ is :

If you're looking to skyrocket your preparation for JEE-2015, then go for solving this set of questions .

Isosceles triangle. Scalane triangle. Right angled triangle. equilateral triangle.

2 solutions

Ankush Tiwari
Mar 24, 2015

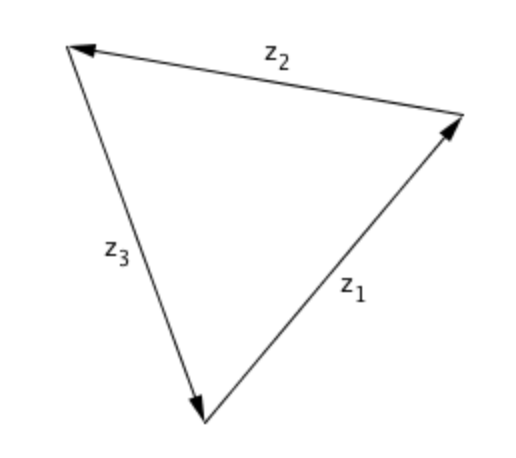
The condition $|z_1|=|z_2|=|z_3|$ implies that the vertices of the triangle are at equal distances from the origin , hence the circumcenter of $ΔABC$ is $O$ .

Also its centroid is

$\frac{z_{1}+z_{2}+z_{3}}{3} = 0$ .

So , the circumcenter and centroid of the triangle coincide and hence it's equilateral.

Nice solution.

Sandeep Bhardwaj - 6 years, 2 months ago

Laurent Shorts
Apr 4, 2016

When drawing $z_1$ , $z_2$ and $z_3$ as vectors one after another to add them, it makes a triangle as their sum is zero. As they have the same norm, it's an equilateral triangle. The angle between each $z_i$ is therefore 120° and it's then easy to see that the triangle they make as vertices is an equilateral one.

A simple triangular Problem.

If you're looking to skyrocket your preparation for JEE-2015, then go for solving this set of questions .

2 solutions

0 pending reports