A sliding conductor reloaded
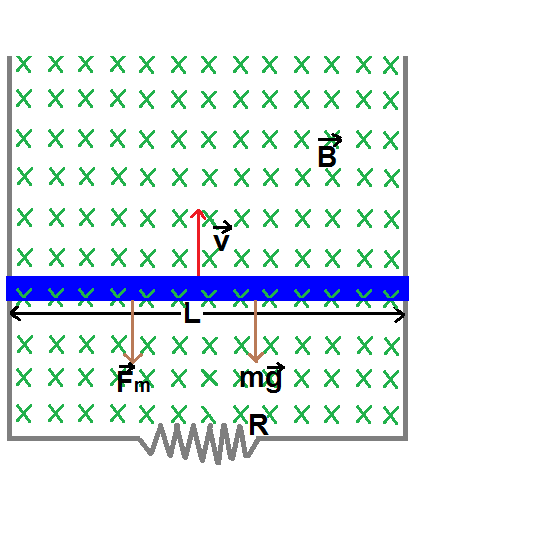 A horizontal conducting rod of mass
m
and length
L
is free to slide on two smooth vertical conducting rails as shown, where there is a magnetic field of intensity
B
directed inside the screen and the resistance of the resistor is
R
.
A horizontal conducting rod of mass
m
and length
L
is free to slide on two smooth vertical conducting rails as shown, where there is a magnetic field of intensity
B
directed inside the screen and the resistance of the resistor is
R
.
The rod is given an initial velocity v 0 upwards. Find the greatest height h that it will attain before falling down. Consider the initial position of the rod as h = 0 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Facepalm !! : − ( Because I didnt think of using a = v d h d v instead just found the time and put it into the height expression. Had to integrate TWICE once for velocity then again for distance. Wasted 2 pages of my book.
Let v be the velocity at any point of the movement of the rod. We see that the induced emf is ϵ = B L v . Then, the current is I = R ϵ = R B L v and the magnetic force, which goes downwards, has a magnitude of F m = I L B = R B 2 L 2 v .
Let a be the acceleration at any point, which will have a direction upwards. So, we have − F m − m g = m a :
− B 2 L 2 v − m g R = m R a
We know that a = d t d v and v = d t d h , hence a = d h v d v and:
− ( B 2 L 2 v + m g R ) = m R v d h d v
Separate the variables:
− m R B 2 L 2 v + m g R v d v = d h
The greatest height will be attained when v = 0 , so we know the limits of integration.
Use the identity b x + c a x = b a ( 1 − b x + c c ) , so we can integrate that:
− B 2 L 2 m R ∫ v 0 0 ( 1 − B 2 L 2 v + m g R m g R ) d v = ∫ 0 h m a x d h
− B 2 L 2 m R [ 0 − v 0 − B 2 L 2 m g R ln ( B 2 L 2 v 0 + m g R B 2 L 2 ( 0 ) + m g R ) ] = h m a x
h m a x = B 2 L 2 m R [ v 0 − B 2 L 2 m g R ln ( m g R B 2 L 2 v 0 + m g R ) ]