A sliding conductor
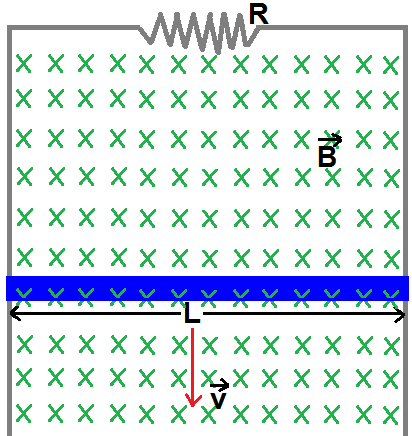 A horizontal conducting rod of mass
m
and length
L
is free to slide on two vertical conducting rails as shown, where there is a magnetised field of intensity
B
directed inside the screen and the resistance of the resistor is
R
. Find the distance travelled by the rod after
t
seconds.
A horizontal conducting rod of mass
m
and length
L
is free to slide on two vertical conducting rails as shown, where there is a magnetised field of intensity
B
directed inside the screen and the resistance of the resistor is
R
. Find the distance travelled by the rod after
t
seconds.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thts brilliant... (+1)
Nicely done!(+1)
Just put t=0. Only one option satisfies
Let v be the velocity at any point of the movement of the rod. We see that the induced emf is ϵ = B L v . Then, the current is I = R ϵ = R B L v and the magnetic force, which goes upwards, has a magnitude of F m = I L B = R B 2 L 2 v .
Now, if we apply Newton's 2nd law we get: m g − F m = m a , which is:
m g − R B 2 L 2 v = m d t d v
This is an easy differential equation, which we can solve as a separable function:
m g R − B 2 L 2 v = m R d t d v
d t = m g R − B 2 L 2 v m R d v
Integrate both sides:
∫ 0 t d t = ∫ 0 v m g R − B 2 L 2 v m R d v
t = − B 2 L 2 m R ln ( m g R − B 2 L 2 v ) ∣ ∣ ∣ 0 v
t = B 2 L 2 m R ln ( m g R − B 2 L 2 v m g R )
Now, solve for v in terms of t :
m R B 2 L 2 t = ln ( m g R − B 2 L 2 v m g R )
e m R B 2 L 2 t = m g R − B 2 L 2 v m g R
m g R e − m R B 2 L 2 t = m g R − B 2 L 2 v
B 2 L 2 v = m g R ( 1 − e − m R B 2 L 2 t )
v = B 2 L 2 m g R ( 1 − e − m R B 2 L 2 t )
Finally, find the distance travelled:
d = ∫ 0 t v d t = B 2 L 2 m g R ( t + B 2 L 2 m R e − m R B 2 L 2 t ) ∣ ∣ ∣ 0 t
d = B 2 L 2 m g R ( t − B 2 L 2 m R ( 1 − e − m R B 2 L 2 t ) )