A sliding equilateral triangle - 2
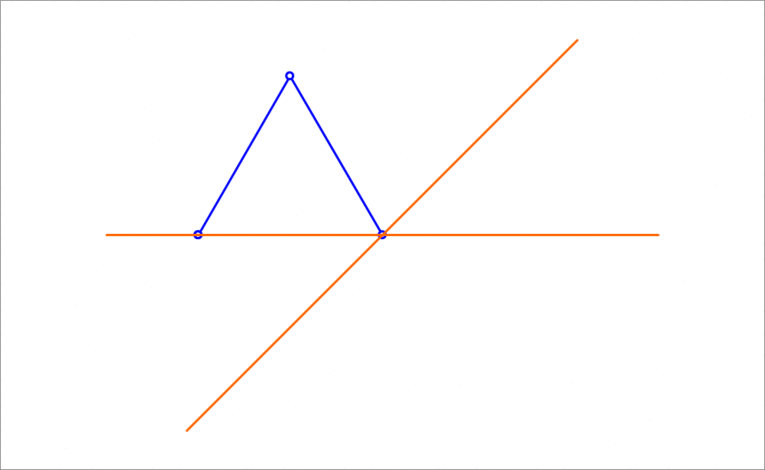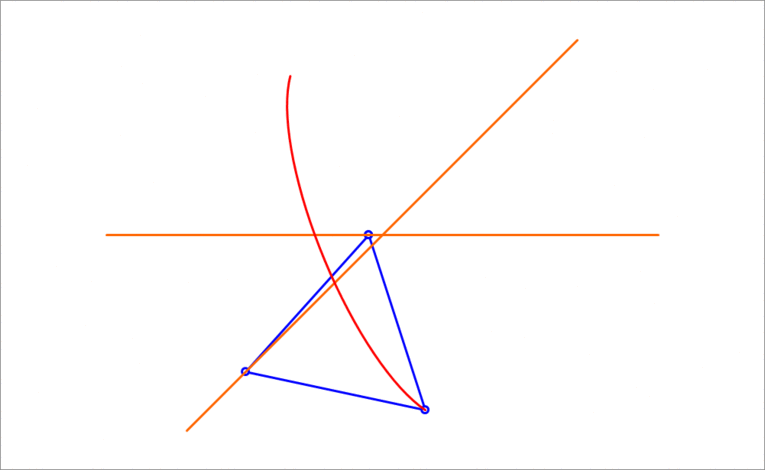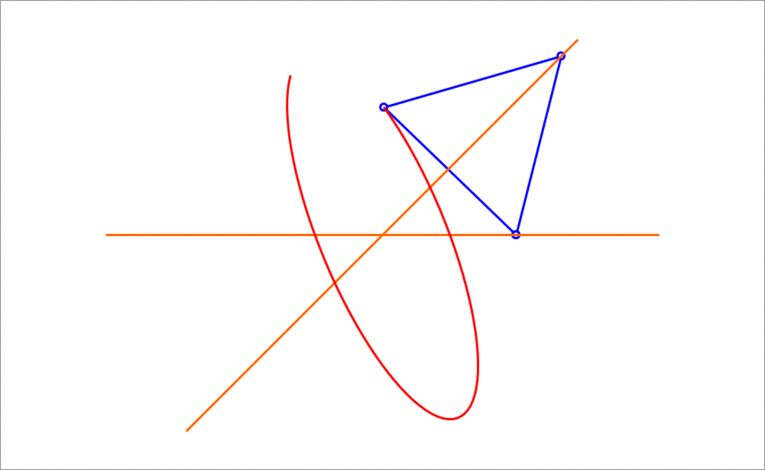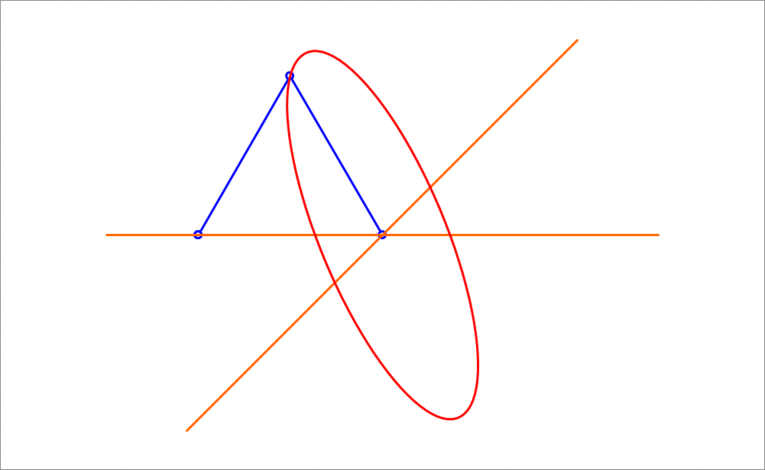
A unit equilateral triangle has two vertices sliding on the orange lines while the third vertex traces a curve, as shown above. The angle between the two orange lines is . The curve generated by the third vertex is an ellipse. Find its area.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By symmetry, the ellipse is centered at the intersection of the two orange lines, and the maximum and minimum distances from this center (the semi-major axis a and and the semi-minor axis b ) occur when the two sliding vertices of the equilateral triangle are equal distances away from this center.
The semi-major axis a can be found by finding A O in the diagram below, when O B = O C and ∠ B O C = 1 3 5 ° .
Since △ B O C is an isosceles triangle, ∠ O B C = 2 1 8 0 ° − 1 3 5 ° = 2 2 . 5 ° . Since BD is half a unit length, BD = \frac{1}{2}. Solving right triangle △ B D O gives D O = 2 1 tan 2 2 . 5 ° = 2 2 − 1 . A D is the height of a unit equilateral triangle, so A D = 2 3 . Therefore, a = A O = D O + A D = 2 2 − 1 + 3 .
The semi-minor axis b can be found by finding A ′ O in the diagram below, when O B ′ = O C ′ and ∠ B ′ O C ′ = 4 5 ° .
Since △ B ′ O C ′ is an isosceles triangle, ∠ O B ′ C ′ = 2 1 8 0 ° − 4 5 ° = 6 7 . 5 ° . Since B'D' is half a unit length, B'D' = \frac{1}{2}. Solving right triangle △ B ′ D ′ O gives D ′ O = 2 1 tan 6 7 . 5 ° = 2 2 + 1 . A ′ D ′ is the height of a unit equilateral triangle, so A ′ D ′ = 2 3 . Therefore, b = A ′ O = D ′ O ′ − A ′ D ′ = 2 2 + 1 − 3 .
Therefore, the area of the ellipse is A = π a b = π ( 2 2 − 1 + 3 ) ( 2 2 + 1 − 3 ) = 2 ( 3 − 1 ) π .