A sliding equilateral triangle
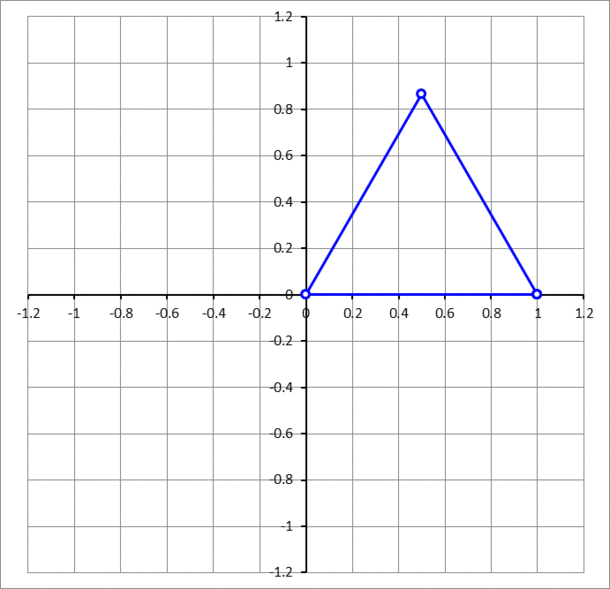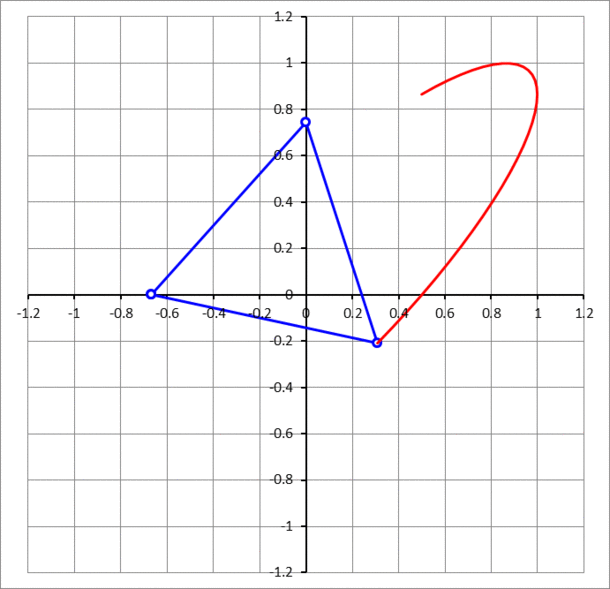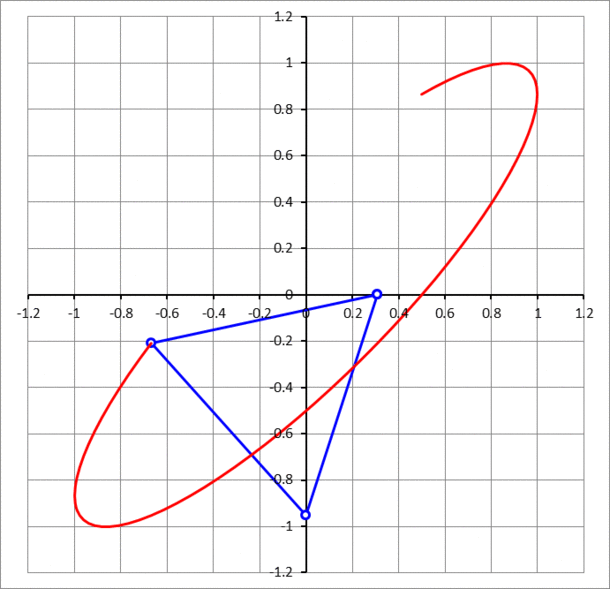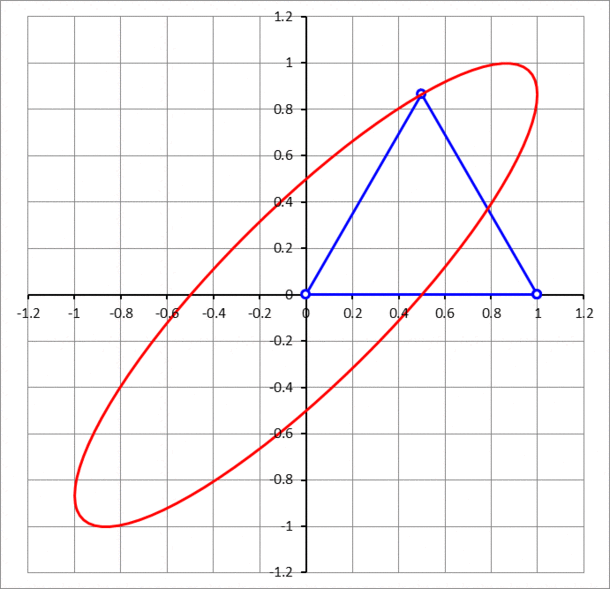
A unit equilateral triangle has two vertices sliding on the - and -axis, while the third vertex traces a curve, as shown above. The curve is an ellipse. Find its area.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of an ellipse is A = π ⋅ a ⋅ b where a is the semi-major axis and b is the semi-minor axis. Thus a is the furthest our vertex gets from the origin, while b is the closest it gets to the origin. We will take advantage of the symmetry of the triangle's movement and the fact that there is only one extreme point in each quadrant: the maximum and minimum distances must occur when the other two vertices are equidistant from the origin.
So the area of the ellipse is π ⋅ a ⋅ b = π ( 2 3 + 2 1 ) ( 2 3 − 2 1 ) = π ⎝ ⎛ ( 2 3 ) 2 − ( 2 1 ) 2 ⎠ ⎞ = π ( 4 3 − 4 1 ) = 2 π