A Slight Deformation 2
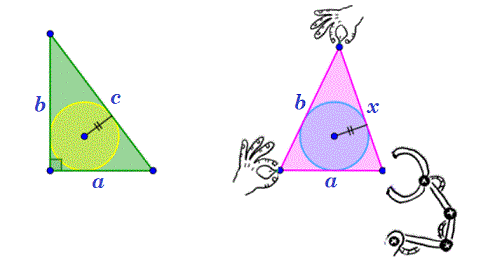
I had a nice right triangle with rational sides a , b , and c such that a + b − c = 1 2 , but someone squeezed it, turning it to an acute one. However, the ex-legs have maintained their lengths ( a and b ) and, surprisingly, the inradius hasn’t changed either. At the same time, the area of the triangle has lost 2 3 ( 5 3 − 1 6 5 7 ) square units. Find the length of the longer leg of the original right triangle.
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
For the first (right) triangle, the semi-perimeter is s 1 = 2 1 ( a + b + c ) , and the area is A 1 = 2 1 a b . For the second (acute) triangle, the semi-perimeter is s 2 = 2 1 ( a + b + x ) , and the area is A 2 = 4 1 ( a + b + x ) ( − a + b + x ) ( a − b + x ) ( a + b − x ) .
Using the equation r = s A we have r = s 1 A 1 = s 2 A 2 , so 2 1 ( a + b + c ) 2 1 a b = 2 1 ( a + b + x ) 4 1 ( a + b + x ) ( − a + b + x ) ( a − b + x ) ( a + b − x ) , which rearranges to:
( a + b + c ) 2 ( x − c ) ( x + a + b ) ( x − 2 1 ( a + b − c + q ) ) ( x − 2 1 ( a + b − c − q ) ) = 0
for q = c 2 + 1 0 ( a + b ) c − 7 ( a + b ) 2 , and has one solution x = 2 1 ( a + b − c + q ) for 0 < x < c .
The difference of areas is then 2 3 ( 5 3 + 1 6 5 7 ) = A 1 − A 2 = 2 1 a b − 4 1 ( a + b + x ) ( − a + b + x ) ( a − b + x ) ( a + b − x ) . Substituting the x and q equations above and simplifying gives 2 3 ( 5 3 + 1 6 5 7 ) = 8 1 ( a + b − c ) ( 3 c − a − b − c 2 + 1 0 ( a + b ) c − 7 ( a + b ) 2 ) . Equating rational parts tells us 2 3 ⋅ 5 3 = 8 1 ( a + b − c ) ( 3 c − a − b ) , and substituting a + b − c = 1 2 and simplifying gives 3 c − a − b = 5 3 . Combining a + b − c = 1 2 and 3 c − a − b = 5 3 gives us c = 2 6 5 and a + b = 2 8 9 .
Using the Pythagorean Theorem on the first (right) triangle now gives a 2 + b 2 = ( 2 6 5 ) 2 . Combining this with a + b = 2 8 9 gives 2 a 2 − 8 9 a + 9 2 4 = 0 and solves to a = 2 8 or a = 2 3 3 , which are the values of the two legs of the right triangle, the longer one being 2 8 .
First, we find the inradius, from the right triangle: r = 2 a + b − c = 6 .
Now we move to the acute △ A B C . Denote I , D , E , F , the incenter and the contact points of the incircle with the triangle, as seen on the figure. Let C B = a , C A = b , ( a < b ) , C D = C F = x , ∠ I C D = ∠ I C F = θ and area of △ A B C = A .
The semiperimeter of △ A B C is s = 2 A B + B C + C A = 2 a + b + ( a + b − 2 x ) = a + b − x ( 1 )
a + b − c = 1 2 ⇒ a + b = 1 2 + c ( 2 )
Hence, A = s ⋅ r = ( a + b − x ) ⋅ 6 ⇒ A = 6 ( 1 2 + c − x ) ( 3 )
( 2 ) ⇒ ( a + b ) 2 = ( 1 2 + c ) 2 ⇒ a 2 + b 2 + 2 a b = ( 1 2 + c ) 2 ⇒ c 2 + 2 a b = ( 1 2 + c ) 2 ⇒ a b = 7 2 + 1 2 c ( 4 )
Again, A = 2 1 C B ⋅ C A ⋅ sin ( 2 θ ) = 2 1 a ⋅ b ⋅ sin ( 2 θ ) = ( 4 ) 2 1 ( 7 2 + 1 2 c ) ⋅ sin ( 2 θ ) ⇒ A = 6 ( 6 + c ) ⋅ sin ( 2 θ ) ( 5 )
( 3 ) , ( 5 ) ⇒ 1 2 + c − x = ( 6 + c ) sin ( 2 θ ) ( 6 )
Alongside,
sin ( 2 θ ) = 1 + cot 2 θ 2 cot θ ( 7 )
From △ C I D we see that cot θ = 6 x ( 8 ) , hence ( 7 ) ⇒ sin ( 2 θ ) = 3 6 + x 2 1 2 x ( 9 )
Combining ( 6 ) , ( 7 ) , ( 8 ) , ( 9 ) and solving for c we get c = x − 6 x 2 − 6 c + 7 2 ( 1 0 )
Since the area loss is 2 3 ( 5 3 − 1 6 5 7 ) , we have 2 1 a b − 6 ( 6 + c ) ⋅ sin ( 2 θ ) = 2 3 ( 5 3 − 1 6 5 7 ) and using ( 4 ) , ( 9 ) and ( 1 0 ) , we find x = 4 7 7 − 1 6 5 7 .
We plug this in ( 1 0 ) to get c = 2 6 5 .
Solving simultaneously ( 2 ) and ( 4 ) we find a = 2 3 3 , b = 2 8