A small garden
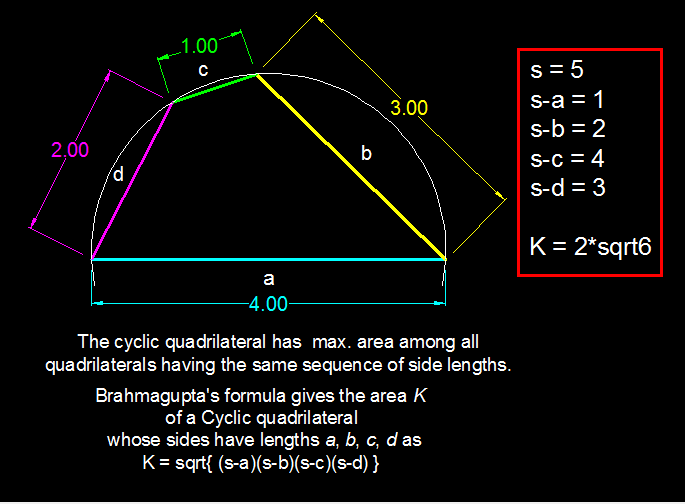
A gardener wants to create a closed fenced field. However, he only has 4 different fencing lengths: one of 1m, one of 2m, one of 3m and one of 4m. If the maximum area that can be fenced can be represented as a b , where a and b are positive integers and b is squarefree, find a + b .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution


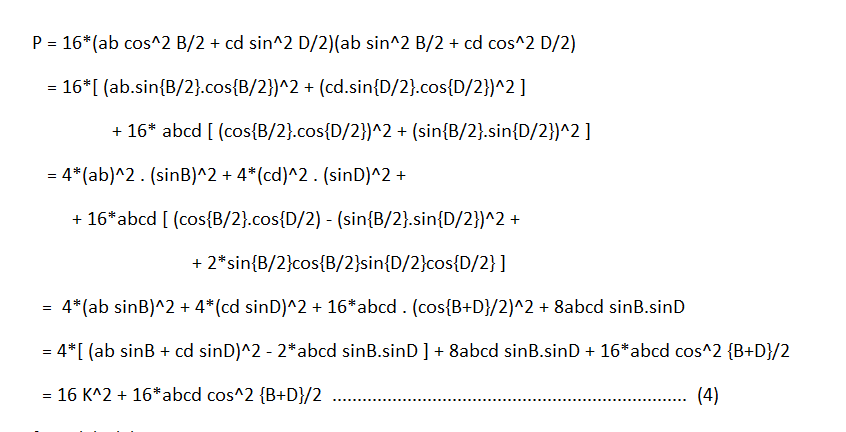
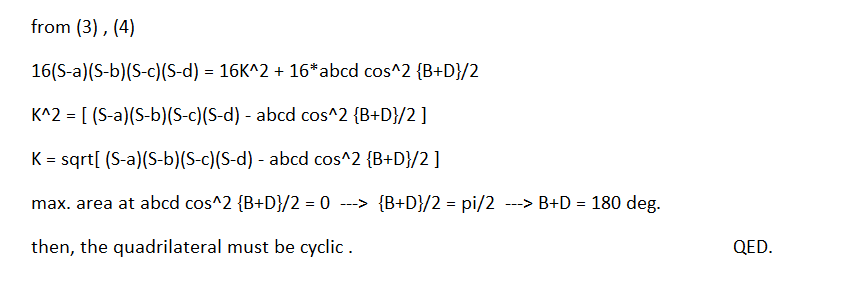
Can you prove your first claim?
Log in to reply
Let me do it XD
Bretschneider's formula states that the area of a quadrilateral is given by ( s − a ) ( s − b ) ( s − c ) ( s − d ) − a b c d ⋅ c o s 2 ( 2 A + C ) where A and C are opposite angles of the quadrilateral. Area is maximised when 2 A + C = 9 0 , which means that the quadrilateral is cyclic.
Log in to reply
Nice! Knocked it out of the park in just a couple of lines.
I've added the proof to my problem solution. Thanks.
Same. Max. with cyclic quadrilateral. Also max with equilateral triangle. Max area given perimeter is square.
If the fence panels could be bent into circular arcs of radius = 1.591549m , it is possible to enclose 7.9577 square meters of area by using a circle. That's quite an improvement over the convex quadrilateral!!