A Special Angle 2
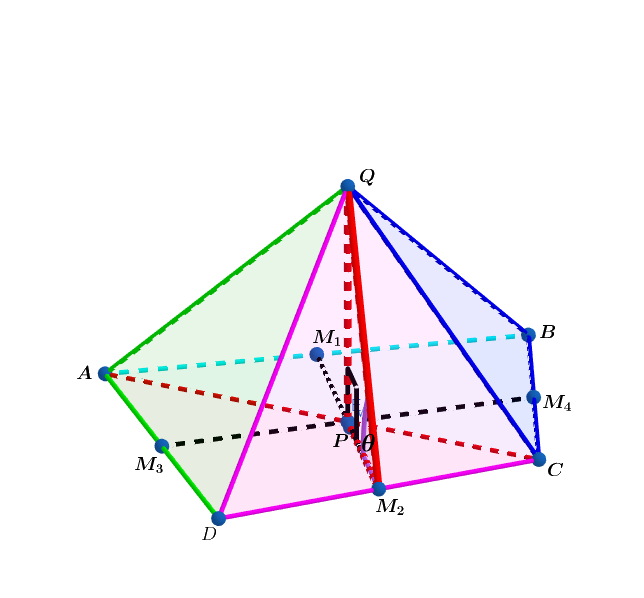
In quadrilateral , and are midpoints of and respectively, and is the centroid of quadrilateral obtained by finding the intersection of the bimedians.
In and .
Let be the height of the pyramid.
Find the value of and that minimizes the triangular face .
Find and express the result to seven decimal places.
:
The answer is 54.7356103.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
△ A B C ≅ △ A D C ⟹ A A B C D = r 1 r 2 sin ( ω ) a 2
The bi-medians of a quadrilateral bisect each other and the diagonals of a quadrilateral are perpendicular ⟹ the bi-medians are congruent ⟹ the centroid P is the midpoint of M 1 M 2 ⟹ P ( 4 2 r 2 cos ( ω ) + r 1 a , 0 ) .
P M 2 = 2 a r 1 2 + 4 r 2 2 sin 2 ( ω ) ⟹ A = A △ Q D C = 4 a r 3 4 h 2 + ( r 1 2 + 4 r 2 2 sin 2 ( ω ) ) a 2
The volume of the pyramid V = 3 1 ( r 1 r 2 sin ( ω ) ) a 2 h = K ⟹ h = r 1 r 2 sin ( ω ) a 2 3 k
Let j = ( r 1 2 r 2 2 sin 2 ( ω ) ) ( r 1 2 + 4 r 2 2 sin 2 ( ω ) ) ⟹ P M 2 = 2 r 1 r 2 sin ( ω ) j a and A ( a ) = r 3 4 r 1 r 2 sin ( ω ) a 3 6 k 2 + j a 6 ⟹ d a d A = r 3 ( 4 r 1 r 2 sin ( ω ) a 2 3 6 k 2 + j a 6 j a 6 − 1 8 k 2 ⟹ a = ( j 3 2 k ) 3 1 ⟹ h = r 1 r 2 sin ( ω ) 3 k ( 3 2 k j ) 3 2
a h = 2 r 1 r 2 sin ( ω ) j ⟹ tan ( θ ) = ( j 2 r 1 r 2 sin ( ω ) ( a h ) = 2 ⟹ θ ≈ 5 4 . 7 3 5 6 1 0 3 .