A Special Locus
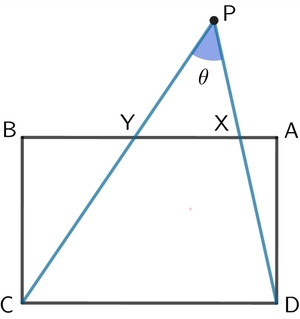 The figure shows a rectangle of side lengths
A
B
=
a
and
B
C
=
b
. A variable point
P
outside the rectangle is made such that
A
X
,
X
Y
and
Y
B
form a geometric progression. If
θ
is the
minimum
measure of
∠
C
P
D
satisfying the conditions, find the expression for
tan
θ
in terms of
a
and
b
. Submit your answer with
a
=
5
and
b
=
3
.
The figure shows a rectangle of side lengths
A
B
=
a
and
B
C
=
b
. A variable point
P
outside the rectangle is made such that
A
X
,
X
Y
and
Y
B
form a geometric progression. If
θ
is the
minimum
measure of
∠
C
P
D
satisfying the conditions, find the expression for
tan
θ
in terms of
a
and
b
. Submit your answer with
a
=
5
and
b
=
3
.
The answer is 1.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The minimum value of θ is different for the cases where 5 a 2 < 9 b 2 .
The expression that you have calculated works only for the cases where 5 a 2 > 9 b 2 .
And, θ can also attain a minimum value for cases where a < b .
Log in to reply
Τhanks for the notes, you are right. Ι have corrected my solution.
Let θ min be the minimum value of θ .
For 5 a 2 < 9 b 2 , tan ( θ min ) = 9 b 2 − a 2 6 a b .
For 5 a 2 > 9 b 2 , tan ( θ min ) = 2 b a + a 2 − b 2 .
Log in to reply
@Digvijay Singh - I think, in the wording of the problem, you should include the restriction that
b
≥
2
a
, otherwise
θ
can get equal to
9
0
∘
and also can take values greater than
9
0
∘
. Since
θ
→
2
π
+
lim
(
tan
θ
)
=
−
∞
,
tan
θ
does not have a minimum in this case.
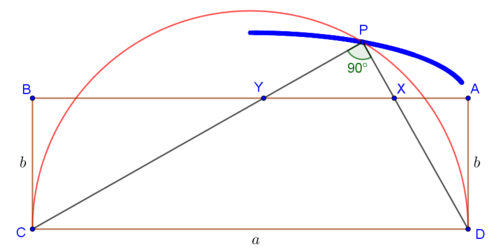
Log in to reply
The question does not ask you to find the minimum of tan θ .
The question asks to find the tangent of the minimum angle θ min , which is always finite, since θ min is always less than 9 0 ∘ .
@Thanos Petropoulos I think you meant △ P E Y ≈ △ C B Y . (third line from the top)
Let the midpoint of A B be at the origin, with A ( 2 1 a , 0 ) , B ( − 2 1 a , 0 ) , C ( − 2 1 a , − b ) , and D ( 2 1 a , − b ) . Also draw P R ⊥ C D with R on C D and Q on A B , and let θ 1 = ∠ C P R and θ 2 = ∠ D P R .
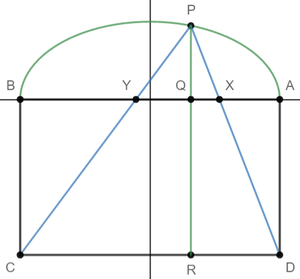
We can show that the locus of points for P lie on the upper half of an ellipse with a major axis of a , a minor axis of b , and centered at the origin:
Using a parametric representation of the ellipse, P will have coordinates P ( 2 1 a cos t , 2 1 b sin t ) .
That means tan θ 1 = P R C R = b + 2 1 b sin t 2 1 a cos t + 2 1 a = b ( 2 + sin t ) a ( 1 + cos t ) and tan θ 2 = P R R D = b + 2 1 b sin t 2 1 a − 2 1 a cos t = b ( 2 + sin t ) a ( 1 − cos t ) .
Since △ P Y X ∼ △ P C D by AA similarity, C D Y X = P R P Q , or a Y X = b + 2 1 b sin t 2 1 b sin t , which solves to Y X = 2 + sin t a sin t .
As alternate interior angles of parallel lines, ∠ B C Y = ∠ Y P R = θ 1 , so that by △ B C Y , B Y = B C tan θ 1 = b ⋅ b ( 2 + sin t ) a ( 1 + cos t ) = 2 + sin t a ( 1 + cos t ) .
Similarly, ∠ X D A = ∠ Q P X = θ 2 , so that by △ X D A , X A = A D tan θ 2 = b ⋅ b ( 2 + sin t ) a ( 1 − cos t ) = 2 + sin t a ( 1 − cos t ) .
Since ( 1 + cos t ) ( 1 − cos t ) = sin 2 t , B Y ⋅ X A = Y X 2 , which means B Y , Y X , and X A are in a geometric progression.
Substituting tan θ 1 = b ( 2 + sin t ) a ( 1 + cos t ) and tan θ 2 = b ( 2 + sin t ) a ( 1 − cos t ) into tan ( θ 1 + θ 2 ) = 1 − tan θ 1 tan θ 2 tan θ 1 + tan θ 2 gives tan θ = b 2 ( 2 + sin t ) − a 2 sin 2 t 2 a b ( 2 + sin t ) .
The minimum and maximum θ values will occur when d t d ( tan θ ) = ( a sin t − b ( sin t + 2 ) ) 2 ( a sin t + b ( sin t + 2 ) ) 2 a b cos t ( ( a 2 − b 2 ) sin 2 t + 4 ( a 2 − b 2 ) sin t − 4 b 2 ) = 0 , which is either at cos t = 0 (which solves to sin t = 1 ), or at ( a 2 − b 2 ) sin 2 t + 4 ( a 2 − b 2 ) sin t − 4 b 2 ) = 0 (which solves to sin t = − 2 + a 2 − b 2 2 a ).
For the latter, since − 1 ≤ sin t ≤ 1 , then − 2 + a 2 − b 2 2 a ≤ 1 which solves to 5 a 2 ≥ 9 b 2 . Some careful analysis of the derivative function shows that the minimum occurs at sin t = 1 when 5 a 2 < 9 b 2 and at sin t = − 2 + a 2 − b 2 2 a when 5 a 2 ≥ 9 b 2 .
Substituting these values of sin t back into tan θ = b 2 ( 2 + sin t ) − a 2 sin 2 t 2 a b ( 2 + sin t ) gives us the following:
-
when 5 a 2 < 9 b 2 , the minimum θ occurs when sin t = 1 , and tan θ min = b 2 ( 2 + 1 ) − a 2 ⋅ 1 2 2 a b ( 2 + 1 ) = 9 b 2 − a 2 6 a b
-
when 5 a 2 ≥ 9 b 2 , the minimum θ occurs when sin t = − 2 + a 2 − b 2 2 a , and tan θ min = b 2 ( a 2 − b 2 2 a ) − a 2 ⋅ ( − 2 + a 2 − b 2 2 a ) 2 2 a b ( a 2 − b 2 2 a ) = 2 b a + a 2 − b 2
In this problem, a = 5 and b = 3 , so 5 a 2 ≥ 9 b 2 , and tan θ min = 2 ⋅ 3 5 + 5 2 − 3 2 = 1 . 5 .
Nice observation that we have an ellipse involved and worth to be brought up. To be more precise, it can be an ellipse with a major axis of a and a minor axis of b or vise versa, or it can even be a circle in case a = b . It is easy to show that only the points of this conic beget the geometric progression, hence the locus is indeed the upper part of the ellipse/circle.
Let Y X = c and their common ratio be p , so that A X = p c and Y B = c p . From that it follows:
c p + c + p c = a
p + 1 + p 1 = c a
( i ) p + p 1 = c a − c
Also, let α and β be marked as follows.
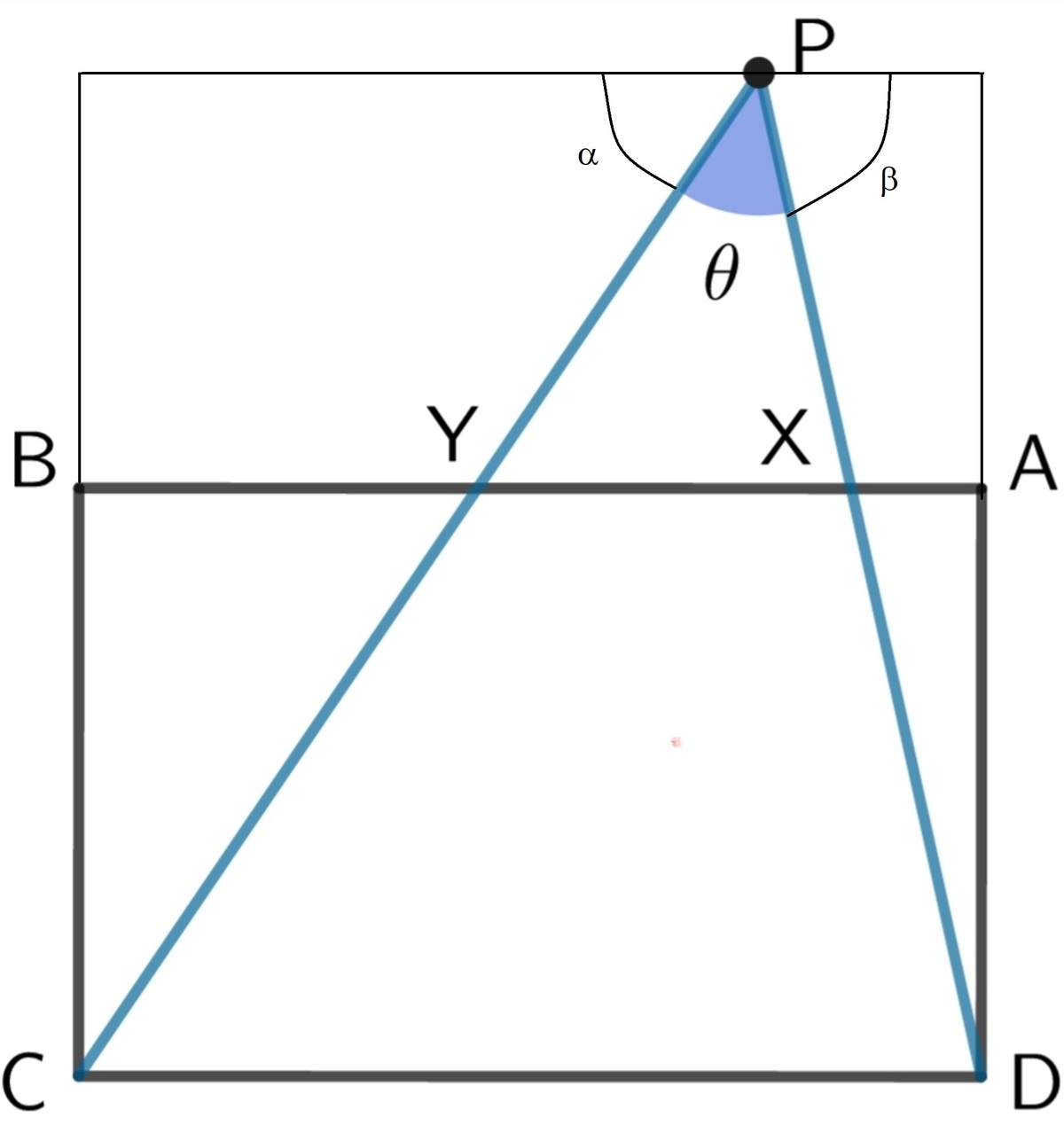
Notice also that ∠ B Y C = α and ∠ A X D = β . So:
tan ( α ) = c p b
tan ( β ) = c b p
So:
tan ( α + β ) = 1 − c p b c b p c p b + c b p
tan ( α + β ) = b ( p + p 1 ) c 2 − b 2 c
Plugging ( i ) into this:
tan ( α + β ) = b ( c a − c ) c 2 − b 2 c
tan ( α + β ) = c 2 − b 2 b ( a − c )
Since θ and α + β add up to 1 8 0 degrees, tan ( θ ) = − tan ( α + β ) :
( i i ) tan ( θ ) = c 2 − b 2 b ( c − a )
To minimize θ is the same as minimize tan ( θ ) , since 0 o < θ < 9 0 o and, in that interval, tan ( θ ) is continuous and increasing . So, differentiating ( i i ) with respect to c , one gets:
( c 2 − b 2 ) 2 b ( c 2 − b 2 ) − ( b c − a b ) 2 c = 0
If c = b , then we can multiply both sides by ( c 2 − b 2 ) 2 . Then:
c 2 − 2 a c + b 2 = 0
[ c − ( a + a 2 − b 2 ) ] ⋅ [ c − ( a − a 2 − b 2 ) ] = 0
Since c < a :
c = a − a 2 − b 2 .
Which makes for the given case:
c = 1
And:
tan ( θ ) = 2 3 = 1 . 5
The question asked to find a general solution. Could you maybe address the general problem rather than the specific one?
Log in to reply
Sorry when I solved it the question was different. I'll edit the answer then
Mr @Digvijay Singh , I've edited it to make it general.
Disclaimer: I've removed a flawed section of my solution because I made a wrong generalization.
To avoid the abuse of notation, I will relabel the vertex A as A ′ .
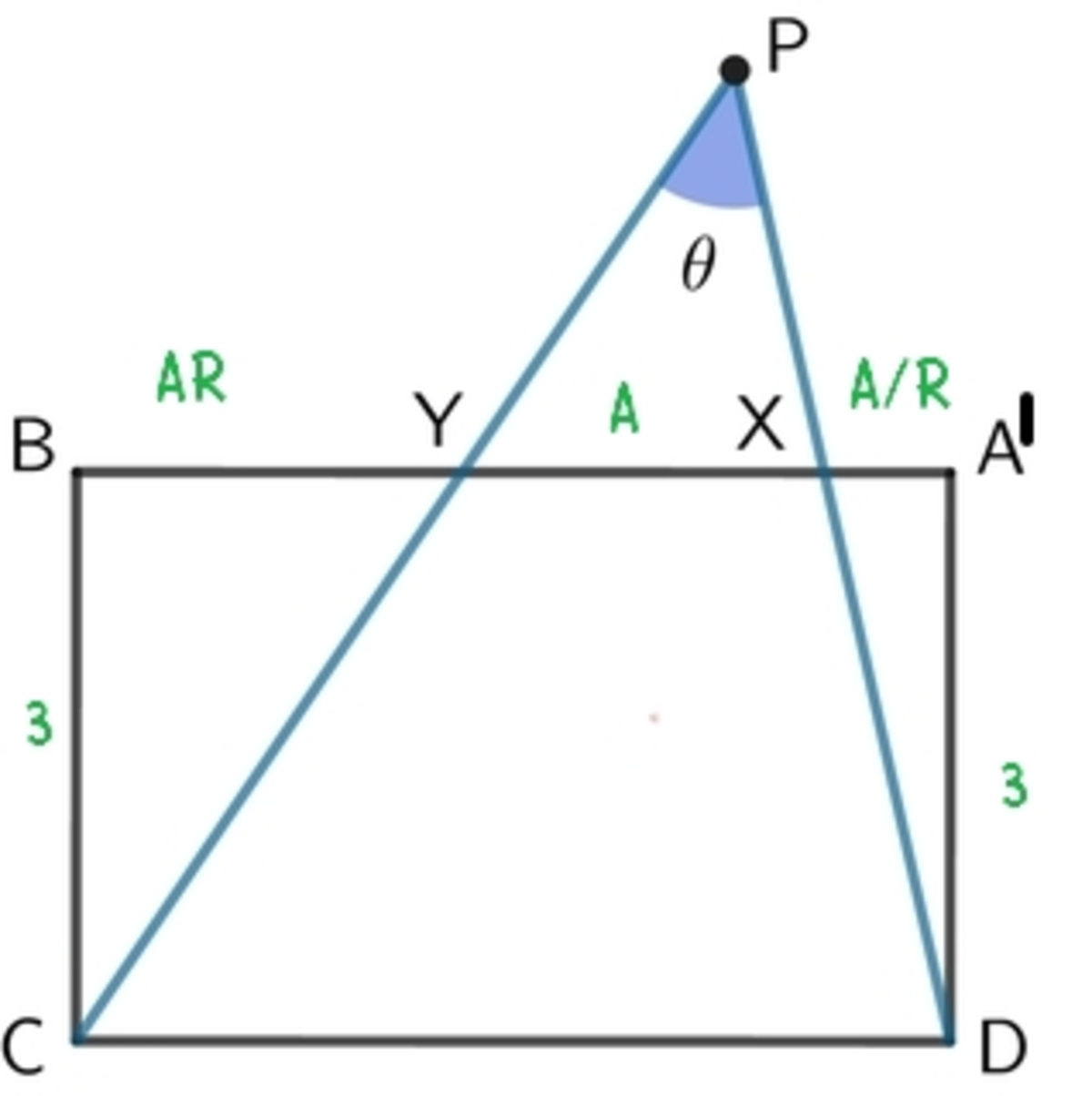
Let ( A ′ X , X Y , Y B ) = ( R A , A , A R ) , where R > 1 and a = A B = R A + A + A R = 5 .
Then,
∠
Y
C
D
=
∠
B
Y
C
=
tan
−
1
(
A
R
3
)
.
Similarly,
∠
X
D
C
=
∠
A
′
X
D
=
tan
−
1
(
A
/
R
3
)
.
With b = 3 . ∠ C P D = π − ∠ Y C D − ∠ X D C = π − [ tan − 1 ( A R 3 ) + tan − 1 ( A / R 3 ) ]
Apply the compound angle formula, tan ( x + y ) = 1 − tan x ⋅ tan y tan x + tan y , the equation above simplifies to ∠ C P D = π − tan − 1 ( R ( A 2 − 9 ) 3 A ( R 2 + 1 ) )
Substitute A = R + 1 / R + 1 5 gives
∠ C P D = π + tan − 1 [ ( 3 R 2 − 2 R + 3 ) ( 3 R 2 + 8 R + 3 ) 1 5 ( R 2 + 1 ) ( R 2 + R + 1 ) ]
So we want to minimize f ( R ) : = ( 3 R 2 − 2 R + 3 ) ( 3 R 2 + 8 R + 3 ) 1 5 ( R 2 + 1 ) ( R 2 + R + 1 ) R > 1
A simple derivative test shows that f ( R ) is minimized when R 2 − 4 R + 1 = 0 ⇒ R = 2 + 3 . Thus, min ( f ( R ) ) = f ( 2 + 3 ) = 2 3 .
Hence, tan ( θ ( 5 , 3 ) ) = min ( ∠ C P D ) = tan [ π + tan − 1 ( 2 3 ) ] = 2 3 = 1 . 5
You're wrong when you say that θ exists only when a > b . It can exist for all rectangles, but the expression for θ will be different for the cases where 5 a 2 < 9 b 2 .
The expression that you have derived works only for rectangles in which 5 a 2 > 9 b 2 .
Can you find the other expression? Firstly, try finding the locus associated with P .
Whooops .... lemme try to rectify it ...
Let E be the foot of the perpendicular to A B from P . Denote A X , X E , E Y , Y B and P E by k , m , n , l and h respectively, as seem on the figure.
Let ∠ X P E = θ 1 and ∠ Y P E = θ 2 .
△ P E X , △ D A X and △ P E Y , △ C B Y are pairs of similar triangles, hence b h = k m = l n ( 1 )
( 1 ) ⇒ k = b h m and l = b h n ( 2 ) Since k m = l m = k + l m + n , ( 1 ) ⇒ b h = k + l m + n ⇒ b h = a − ( m + n ) m + n ⇒ h m + h n = b a − ( m + n ) ( 3 ) From the geometric progression,
Y X B Y = X A Y X ⇒ Y X 2 = X A ⋅ B Y ⇒ ( m + n ) 2 = k l ⇒ ( 2 ) ( m + n ) 2 = b 2 ⋅ h m ⋅ h n ⇒ h m ⋅ h n = b 2 ( m + n ) 2 ( 4 ) Now, we have
tan θ = 1 − tan θ 1 ⋅ tan θ 2 tan θ 1 + tan θ 2 = 1 − h m ⋅ h m h m + h n = ( 3 ) , ( 4 ) 1 − b 2 ( m + n ) 2 b a − ( m + n ) = b b 2 − ( m + n ) 2 a − ( m + n ) Setting x = m + n , we have a function for tan θ in terms of x :
f ( x ) = b b 2 − x 2 a − x For the domain of f we claim that dom ( f ) = ( 0 , 3 a ] .
Proof: Let r be the common ratio of the geometric progression, i.e. x l = k x = r > 0 . Then, l = r x , k = r x , thus we have l + x + k = a ⇒ r x + x + r x = a ⇒ x = r 2 + r + 1 r a An easy study of the function g ( r ) = r 2 + r + 1 r shows that its range is ran ( g ) = ( 0 , 3 1 ] , hence the domain of f is ( 0 , 3 a ] .
The derivative of f is
f ′ ( x ) = ( b 2 − x 2 ) 2 b ( − x 2 + 2 a x − b 2 )
The discriminant of the quadratic is Δ = 4 ( a 2 − b 2 ) .
Case 1 : a ≤ b
Then Δ ≤ 0 and f ′ ( x ) < 0 for all x ∈ ( 0 , 3 a ) with an exception of a single root if Δ = 0 . Hence f is a decreasing function and, since f is continuous, its range is [ f ( 3 a ) , x → 0 + lim f ( x ) ) Hence,
f min = f ( 3 a ) = b b 2 − ( 3 a ) 2 a − 3 a = 9 b 2 − a 2 6 a b
Case 2 : a > b
Then,
− x 2 + 2 a x − b 2 = 0 ⇔ x = − 2 − 2 a ± 2 a 2 − b 2 = a ∓ a 2 − b 2 The value x = a + a 2 − b 2 is greater than a , hence it is rejected, therefore the only value we have to deal with is x = a + a 2 − b 2 .
Case 2i : a − a 2 − b 2 ≥ 3 a Then, 3 2 a ≥ a 2 − b 2 ⇒ 4 a 2 ≥ 9 a 2 − b 2 ⇒ 5 a 2 ≤ 9 b 2 and in this case − x 2 + 2 a x − b 2 < 0 for all x ∈ ( 0 , 3 a ) , thus, like in case 1, f is a decreasing function and f min = 9 b 2 − a 2 6 a b .
Case 2ii : a − a 2 − b 2 < 3 a ⇔ 5 a 2 > 9 b 2
Then f has a minimum at x 0 = a − a 2 − b 2 , because f ′ ( x ) < 0 for x ∈ ( 0 , x 0 ) and f ′ ( x ) > 0 for x ∈ ( x 0 , 3 a ] .
The minimum value is
f min = f ( a − a 2 − b 2 ) = b 2 − ( a − a 2 − b 2 ) 2 b a 2 − b 2 = b 2 − a 2 + b 2 + 2 a a 2 − b 2 b a 2 − b 2 = b 2 − a 2 + b 2 + 2 a a 2 − b 2 b a 2 − b 2 = 2 1 ⋅ a 2 − b 2 ( a − a 2 − b 2 ) b a 2 − b 2 = 2 1 ⋅ ( a − a 2 − b 2 ) b = 2 ( a 2 − a 2 + b 2 ) b ( a + a 2 − b 2 ) = 2 b a + a 2 − b 2
With a = 5 and b = 3 we are in case 2ii, hence our answer is: f min = 2 × 3 5 + 5 2 − 3 2 = 2 3 = 1 . 5