A special triangle corrected
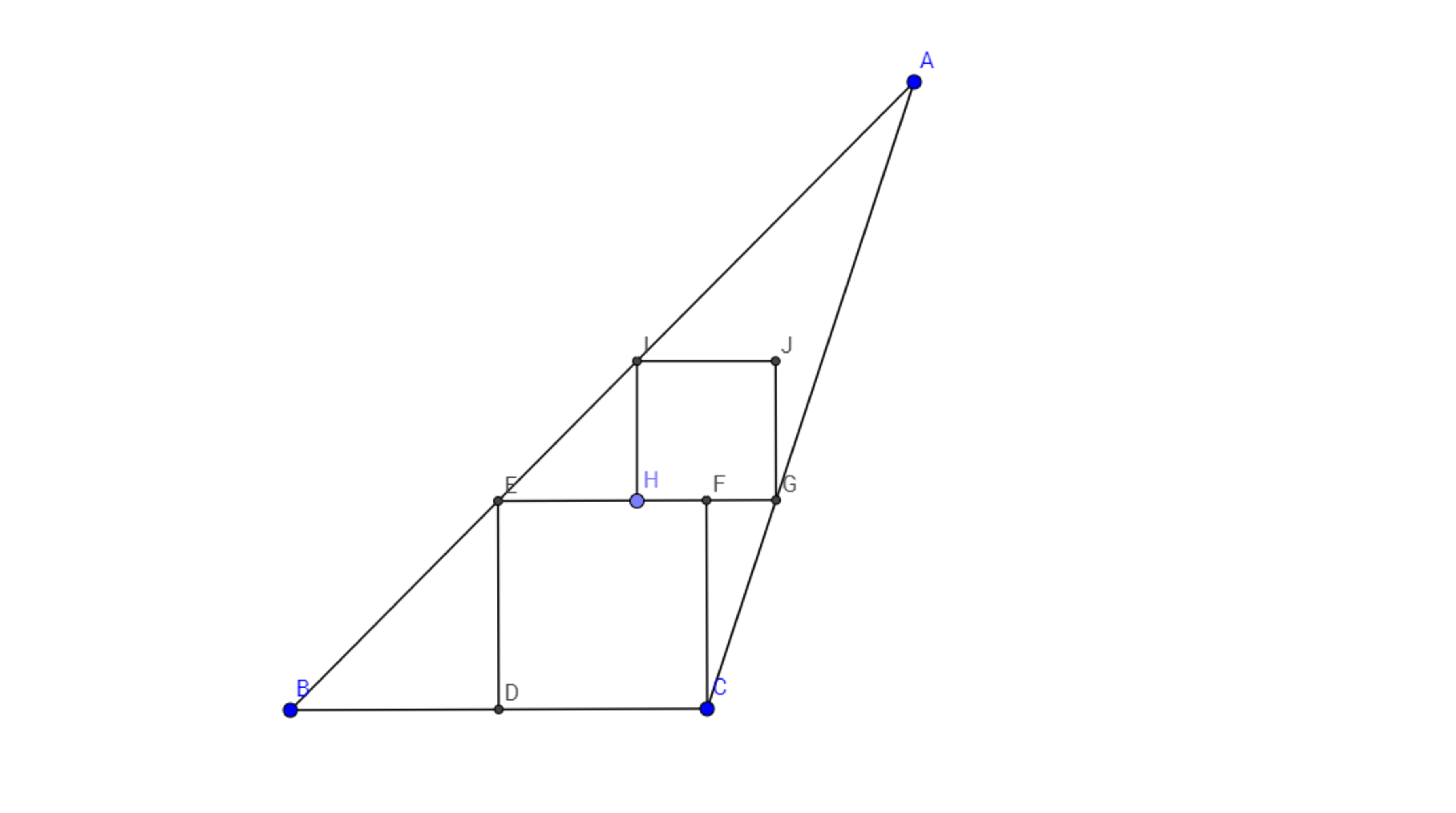
In a triangle A B C as shown in the above diagram with B C = 1 , a rectangle C D E F is formed where D is the midpoint of B C , point E lies on A B and point F lies inside triangle A B C . Interestingly, rectangle C D E F turns out to be a square.
Next another rectangle G H I J is constructed such that point G is where line E F extended meets A C , H is another point on E F such that H F = F G , I lies on A B and J lies inside triangle A B C . Even more interestingly, rectangle G H I J also turns out to be a square.
Now determine the reciprocal of the area of triangle C F G .
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Considering that B C = 1 , with D as the midpoint of B C , we have B D = C D = 2 1 . Then C D E F being a square means D E = E F = C F = C D = 2 1 . Let F G = x . Then H F = F G = x as given in the question which means E H = E F − H F = 2 1 − x .
Now note that B D E and E H I are similar triangles as B D and E H are parallel and so are D E and H I . Therefore H I E H = D E B D = 1 which means H I = E H = 2 1 − x . Considering G H I J is also a square, G H = H I = 2 1 − x . Moreover, G H = H F + F G = x + x = ( 1 + 1 ) x = 2 x . Therefore:
2 x = 2 1 − x
2 x + x = 2 1
( 2 + 1 ) x = 2 1
3 x = 2 1
x = 3 × 2 1
x = 6 1
Therefore, the area of C F G = 2 1 × C F × F G = 2 1 × 2 1 × 6 1 , the reciprocal of which is 2 × 2 × 6 = 4 × 6 = 2 4
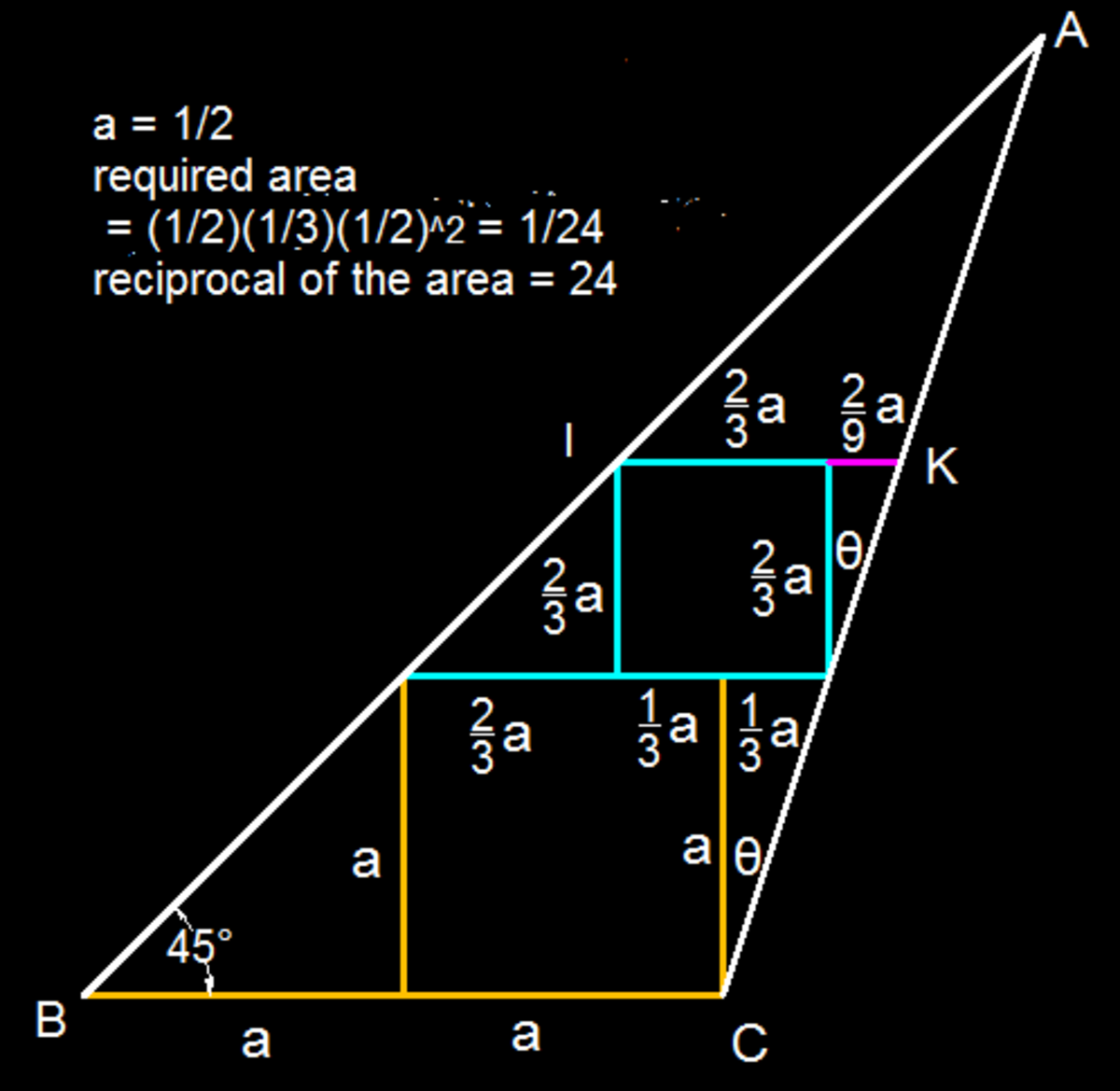
C F = D C = 2 1
Let side of small square be I H = a
Ratio B D E D = 1 , therefore H E I H = 1 and H E = a
H F = F G = 2 a
E F = E H + H F = a + 2 a = 2 3 a
But we know that E F = 2 1 , that gives us the equation for a as: 2 3 a = 2 1 and a = 3 1
F G = 2 a = 6 1
Area [ C F G ] = 2 1 × C F × F G = 2 1 × 2 1 × 6 1 = 2 4 1
Inverse of the area is: 2 4