A sphere between two parallel planes. How many spheres can be added?

This problem's question: How many more spheres can be added?

There are additional conditions and definitions. A sphere is the boundary of a closed ball. There are two spheres within the larger sphere. The sum of the radii of the two interior spheres does not have to equal the radius of the exterior sphere. All of these spheres have positive radii and are mutually tangent (in contact). The added spheres must be tangent to all of the original three spheres and except for the first added sphere, must be tangent to at least one of the added spheres. Tangency is the only form of contact permitted by any of the spheres, original or added. Crossing through a sphere (the boundary of a ball) is not permitted. A sphere expanded to a infinite radius becomes a plane. In the situation of two balls within another sphere,one of the inside spheres must grow to a plane also with the tangency of the two planes at infinity around the still small sphere meeting the tangency requirement of the planar spheres.

The added spheres do not have to have , but may have, the same radii. Only requirement is that the added spheres meet the tangency requirements.

Some people apparently are having understanding the static pictures, therefore, the pictures have been remade as animated GIFs and the colors made consistent.

Before expansion:

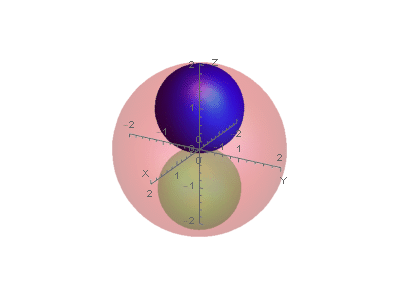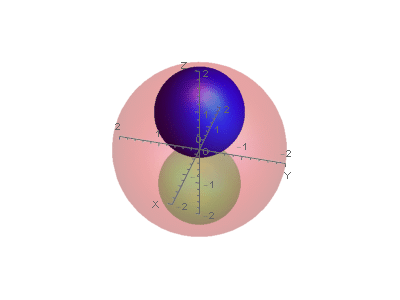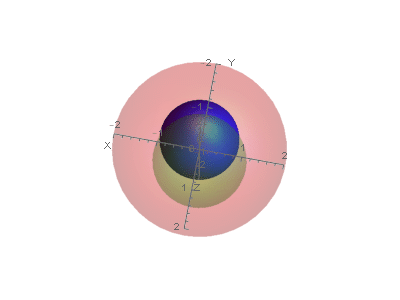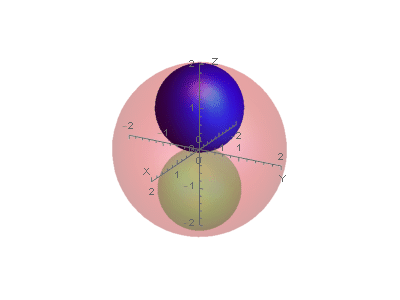
After expansion:

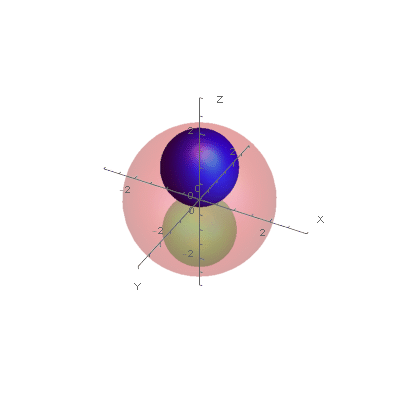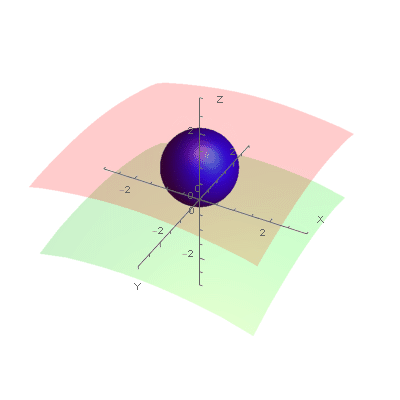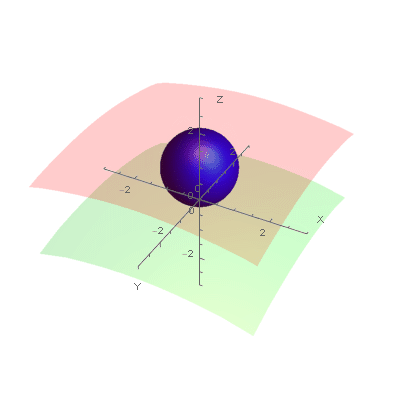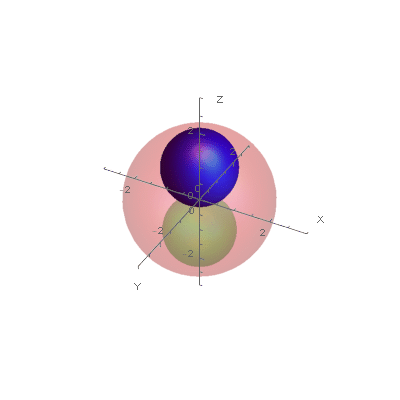
This is a permissible nesting of the original spheres.