A sphere with a through cylindrical hole
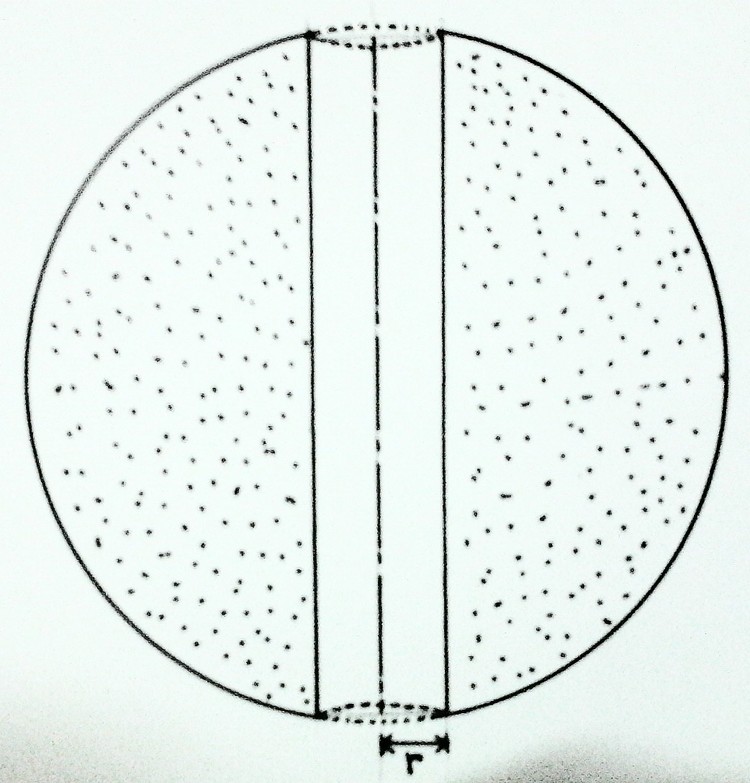 The picture above shows a solid sphere having a radius
R
& a cylindrical hole with a radius
r
thoroughly drilled along the diameter. If
R
r
=
6
1
then find out the ratio of volume of the drilled sphere to that of the original sphere (without hole).
The picture above shows a solid sphere having a radius
R
& a cylindrical hole with a radius
r
thoroughly drilled along the diameter. If
R
r
=
6
1
then find out the ratio of volume of the drilled sphere to that of the original sphere (without hole).
The answer is 0.958624038.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
By using integration, we can easily find out the simplest expression, for calculating the volume ( V d r i l l e d ) of a sphere, with a radius R , having a cylindrical hole with a radius r drilled along the diameter, given as follows V d r i l l e d = 3 4 π ( R 2 − r 2 ) 2 3 Where, 0 ≤ r < R . Hence, the ratio of the volume of drilled sphere to that of the original sphere is = 3 4 π R 3 V d r i l l e d = 3 4 π R 3 3 4 π ( R 2 − r 2 ) 2 3 = ( 1 − ( R r ) 2 ) 2 3 = ( 1 − ( 6 1 ) 2 ) 2 3 = ( 3 6 3 5 ) 2 3 ≈ 0 . 9 5 9
I'm realy proud of myself because I solved this problem after hard effort without using any integration (unlike other solutions here) , because I haven't studied it yet .
just use this 4/3 pie R^3 - pie r^2 (2R) over 4/3 pie R^3.........the 2R is due to the height of cylinder is 2 R of the sphere
I found out that there is a simpler geometric way of solving this, and a calculus method. I shall demonstrate both:
1. Geometric Approach:
Start off by determining the the volume of the original sphere (without the hole), is given by the formula for the volume of the sphere:
V S = 3 4 π R 3 where R = Sphere radius
Now we need to find the volume of the drilled sphere. You need to realize that the volume of the drilled sphere must be: (Volume of original sphere) − (Volume of empty cylinder)
The equation for the volume of a cylinder is given by:
V C = π r 2 h r = Cylinder radius, h = Cylinder height
Substituting in r = 6 R and h = 2 R :
V C = π ( 6 R ) 2 ( 2 R ) = 1 8 π R 3
Thus, the volume of the drilled sphere must be:
V d r i l l = V S − V C = 3 4 π R 3 − 1 8 π R 3 = 1 8 2 3 π R 3
The ratio of the volume of the drilled sphere to the volume of the original sphere is then given by:
(Volume of original sphere) (Volume of drilled sphere) = 3 4 π R 3 1 8 2 3 π R 3 = 2 4 2 3 ≈ 0 . 9 5 9
This approximation only works for r < < R
2. Calculus Approach:
To do this, we will utilize the power of the washer method, which defines the volume of rotation about an axis defined as a difference of two functions is:
V = π ∫ a b ( Outer Radius ) 2 − ( Inner Radius ) 2 d x
If we are to take a vertical slice of the sphere in the 1st quadrant, we recieve the equation of the quarter circle defined by the slice as:
f ( x ) = + R 2 − x 2
where R is the radius of the sphere, and we take the positive root as we are in the first quadrant. We should also notice that with this method, the slice of the cylinder will be defined as the vertical line x = r where r is the cylinder's radius.
Since are trying to find horizontal disks that are created by revolving our functions around the y-axis, we will need to find inverse so that y is our variable, because the rectangles formed to construct the disk lie parallel to the x-axis. (Comment if that doesn't make too much sense; a diagram would probably be good, but I don't know how to make one online)
Luckily for us, the equation of the cylinder is always a constant function of y. Luckily once more, the inverse of our quarter circle is also very simple:
f ( y ) = + R 2 − y 2 g ( y ) = r = 6 R
When integrating with respect to the y-axis, you must subtract the function closer to the y-axis from the one that is farther. As we can see in the given picture, the sphere is on the "right" side of the cylinder, up until the point x = r or f ( r ) = R 2 − r 2 = R 2 − 3 6 R 2 = 3 6 3 5 R 2 = 6 R 3 5 , where the hole begins to touch the sphere. The bounds when integrating with respect to y are from the smallest y value attained to the largest. Putting this all together we get:
V = π ∫ 0 6 R 3 5 ( f ( y ) ) 2 − ( g ( y ) ) 2 d y = π ∫ 0 6 R 3 5 ( R 2 − y 2 ) 2 − ( 6 R ) 2 d y = π ∫ 0 6 R 3 5 R 2 − y 2 − 3 6 R 2 d y = π ∫ 0 6 R 3 5 3 6 3 5 R 2 − y 2 d y = π ( 3 6 3 5 y R 2 − 3 y 3 ) ∣ ∣ ∣ ∣ ∣ 0 6 R 3 5 π ( 2 1 6 3 5 3 5 R 3 − 6 4 8 3 5 3 5 R 3 ) = 3 2 4 3 5 π 3 5 R 3
This is the volume of half of the drilled sphere as we have only rotated formed a figure in the upper quadrants. Thus the ratio would be the same whether we double this value, or half the value of the original sphere. We choose the latter:
(Half of Volume of original sphere) (Half of Volume of drilled sphere) = 3 2 π R 3 3 2 4 3 5 π 3 5 R 3 = 2 1 6 3 5 3 5 ≈ 0 . 9 5 9