A spherical area bounded by three arcs
Taking the unit sphere in the first octant, we define three curves parallel to the x y , x z and y z planes, parametrically, as follows:
p 1 ( t ) = ( sin θ 0 cos t , sin θ 0 sin t , cos θ 0 ) , 0 ≤ t ≤ 2 π
p 2 ( s ) = ( sin θ 0 cos s , cos θ 0 , sin θ 0 sin s ) , 0 ≤ s ≤ 2 π
p 3 ( r ) = ( cos θ 0 , sin θ 0 cos r , sin θ 0 sin r ) , 0 ≤ r ≤ 2 π
If θ 0 = 8 1 ∘ , then find the area bounded by the three arcs on the surface of the sphere, (shaded in yellow)
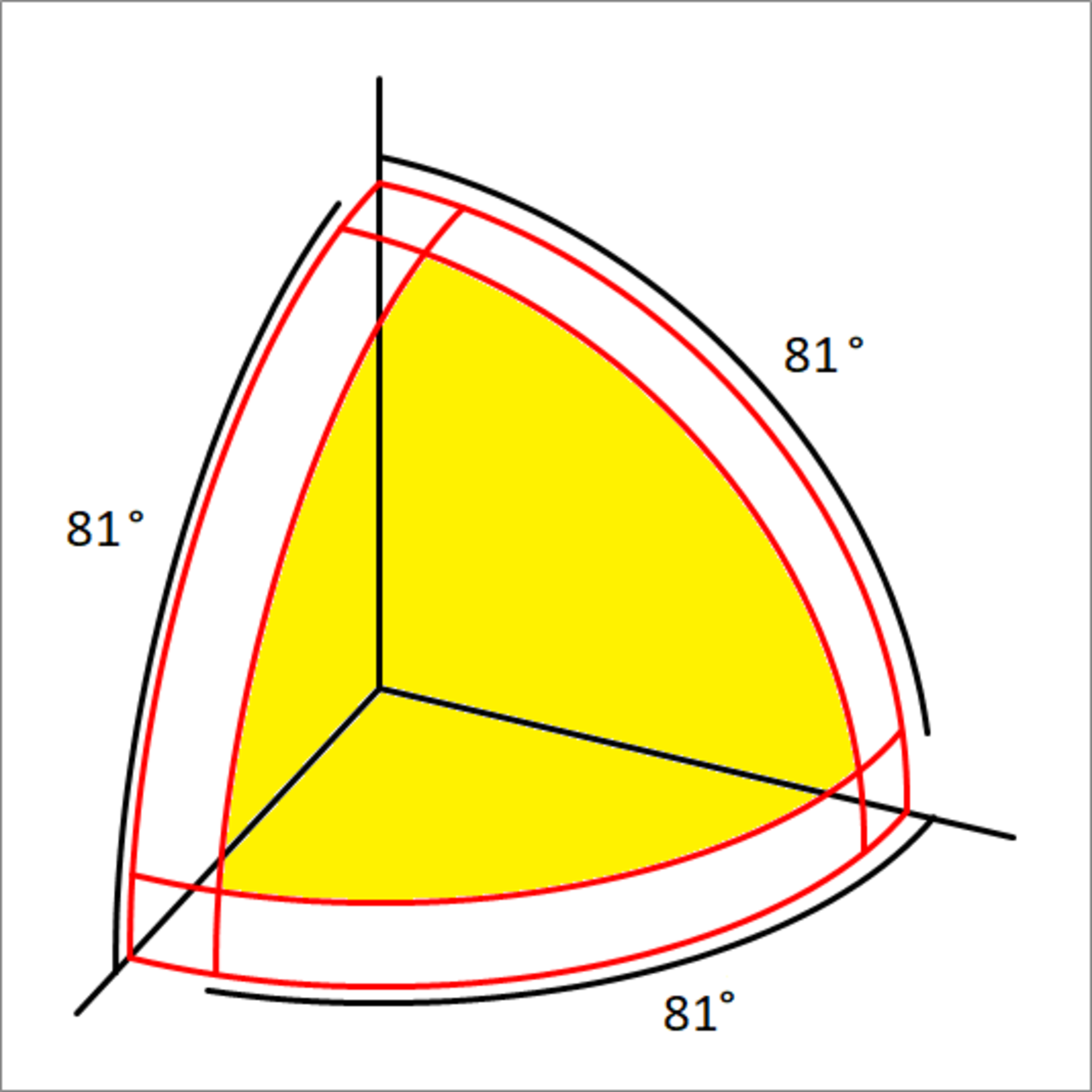
The answer is 0.9076.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I find angle A=B=C=88.5 degree for sphere triangle and use area from https://mathworld.wolfram.com/SphericalTriangle.html - but it not true. It is not three great circular arcs.
Monte Carlo with Phyton.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
We're going to consider the area shaded in light blue in the figure above. It is 6 1 of the required
area (from symmetry). To compute its area we'll define the green arc as the great arc (center at the origin) and characterized by y = z , and the blue arc as the great arc (center at the origin) characterized by x = y .
Blue Area = ∫ ϕ = ϕ 1 4 π ∫ θ = θ 1 θ 0 sin θ d θ d ϕ
where ϕ 1 is characterized by sin θ 0 sin ϕ 1 = cos θ 0
Therefore, ϕ 1 = sin − 1 ( cot θ 0 )
And sin θ 1 sin ϕ = cos θ 1 (since y = z ), thus θ 1 = tan − 1 ( sin ϕ 1 )
After integration with respect to θ , the above integral becomes,
Blue Area = ∫ ϕ = ϕ 1 4 π ( cos θ 1 − cos θ 0 ) d ϕ
Since tan θ 1 = sin ϕ 1 then cos θ 1 = 1 + sin 2 ϕ sin ϕ
Hence, the integral becomes,
Blue Area = cos θ 0 ( ϕ 1 − 4 π ) + ∫ ϕ = ϕ 1 4 π 1 + sin 2 ϕ sin ϕ d ϕ
Substituting sin 2 ϕ = 1 − cos 2 ϕ , the integral becomes,
Blue Area = cos θ 0 ( ϕ 1 − 4 π ) + ∫ ϕ = ϕ 1 4 π 2 − cos 2 ϕ sin ϕ d ϕ
Blue Area = cos θ 0 ( ϕ 1 − 4 π ) + ∫ ϕ = ϕ 1 4 π 2 1 − ( cos ϕ / 2 ) 2 sin ϕ d ϕ
Using the substituting u = 2 cos ϕ , the integral becomes
Blue Area = cos θ 0 ( ϕ 1 − 4 π ) + sin − 1 ( cos ϕ 1 / 2 ) − 6 π
Hence, finally, the required area is 6 times the above expression, and is given by
Area = 6 ( cos θ 0 ( ϕ 1 − 4 π ) + sin − 1 ( cos ϕ 1 / 2 ) − 6 π )