A square, a rhombus, and five tangent circles
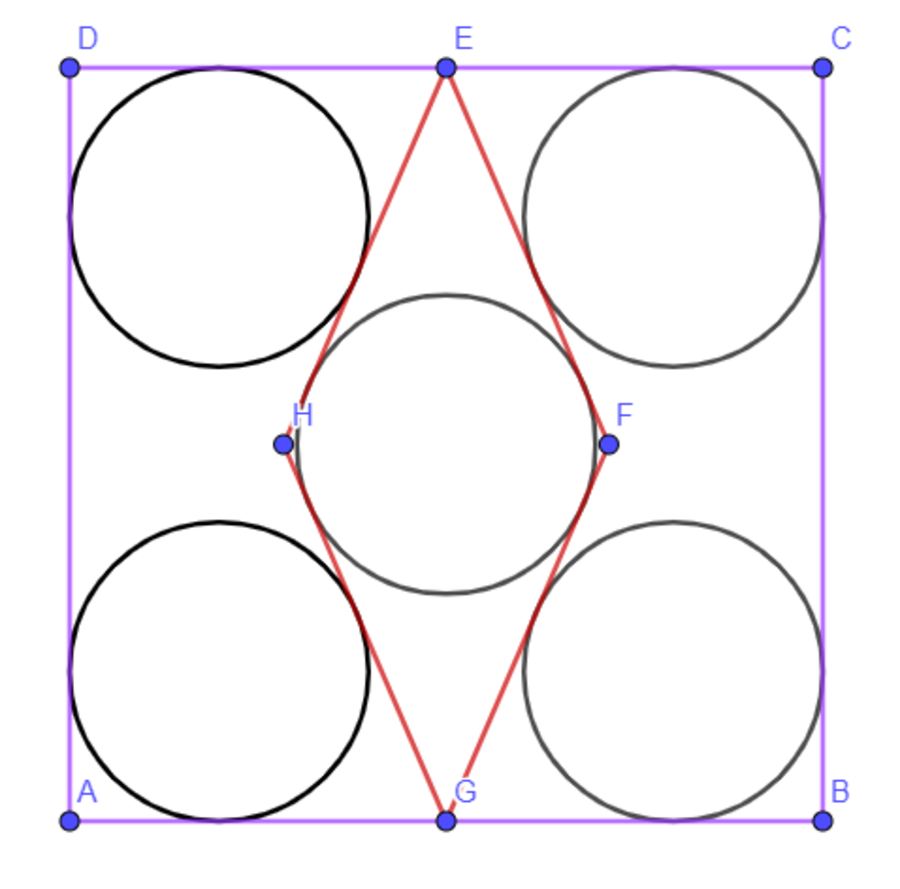
The figure above depicts square A B C D of side length 8 . Taking E as the midpoint of the upper side and G as the midpoint of the bottom side, we draw rhombus E F G H as shown. The rhombus is drawn such that its incircle and the four corner circles tangent to it are all congruent. Find the radius of each of these five circles.
The answer is 1.5864.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
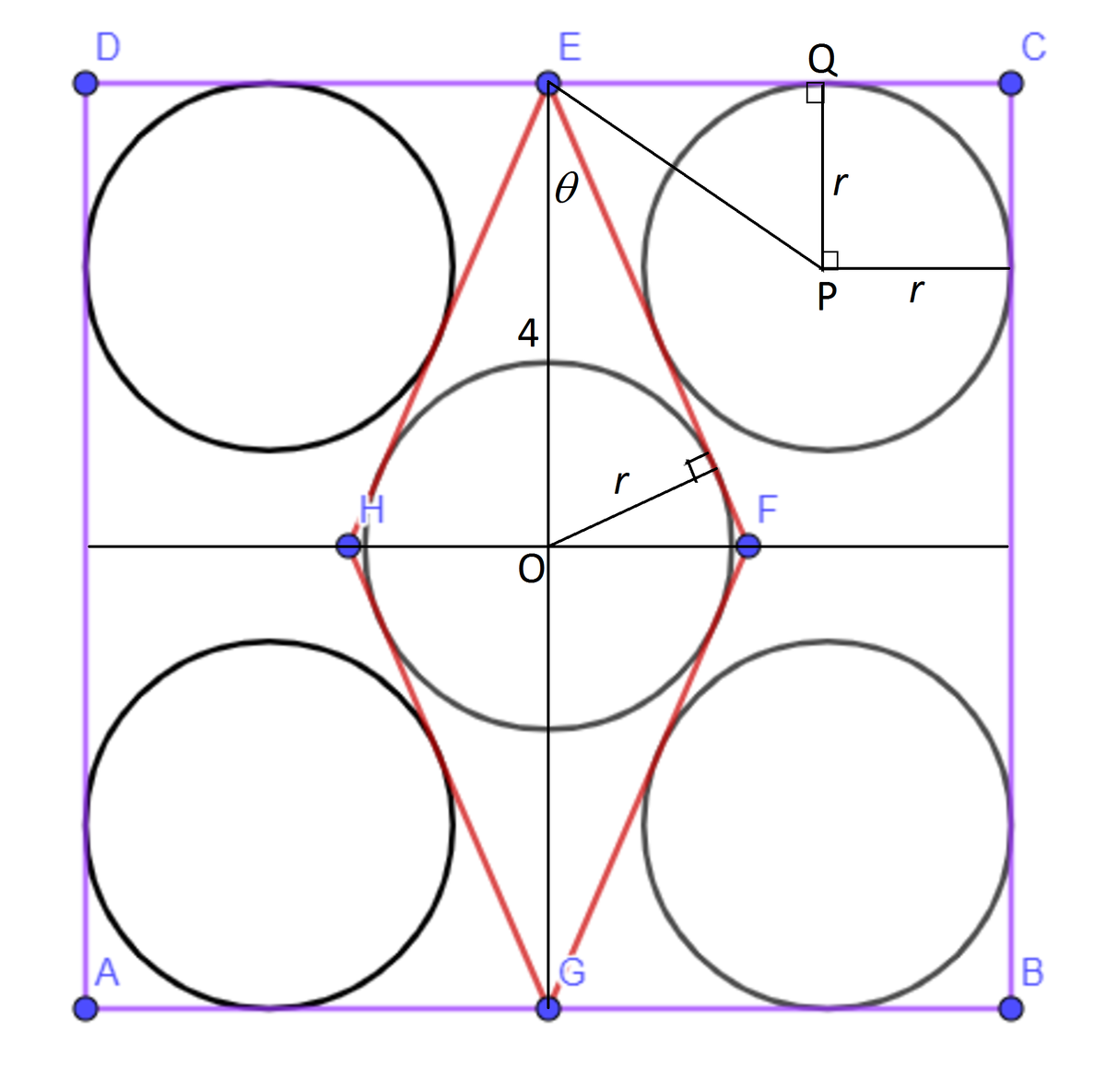
Let the radius of the five circles be r , centers of the center circle and the top right circle be O and P respectively, P Q be perpendicular to C E and ∠ O E F = θ . Then we note that sin θ = 4 r . And
P Q cot ∠ P E Q + Q C r cot ( 2 9 0 ∘ − θ ) + r tan ( 4 5 ∘ + 2 θ ) + 1 1 − t 1 + t + 1 1 − t 2 t 3 − t 2 + 5 t − 1 ⟹ t r = C E = 4 = r 4 = sin θ 1 = 2 t 1 + t 2 = 2 t 1 + t 2 = 0 = 3 1 + 3 − 2 7 8 + 9 2 7 8 + 3 − 2 7 8 − 9 2 7 8 ≈ 0 . 2 0 6 7 8 3 4 9 5 = 4 sin θ = 1 + t 2 8 t ≈ 1 . 5 9 Divide both sides by r Note that sin θ = 4 r Let t = tan 2 θ By Cardano’s method
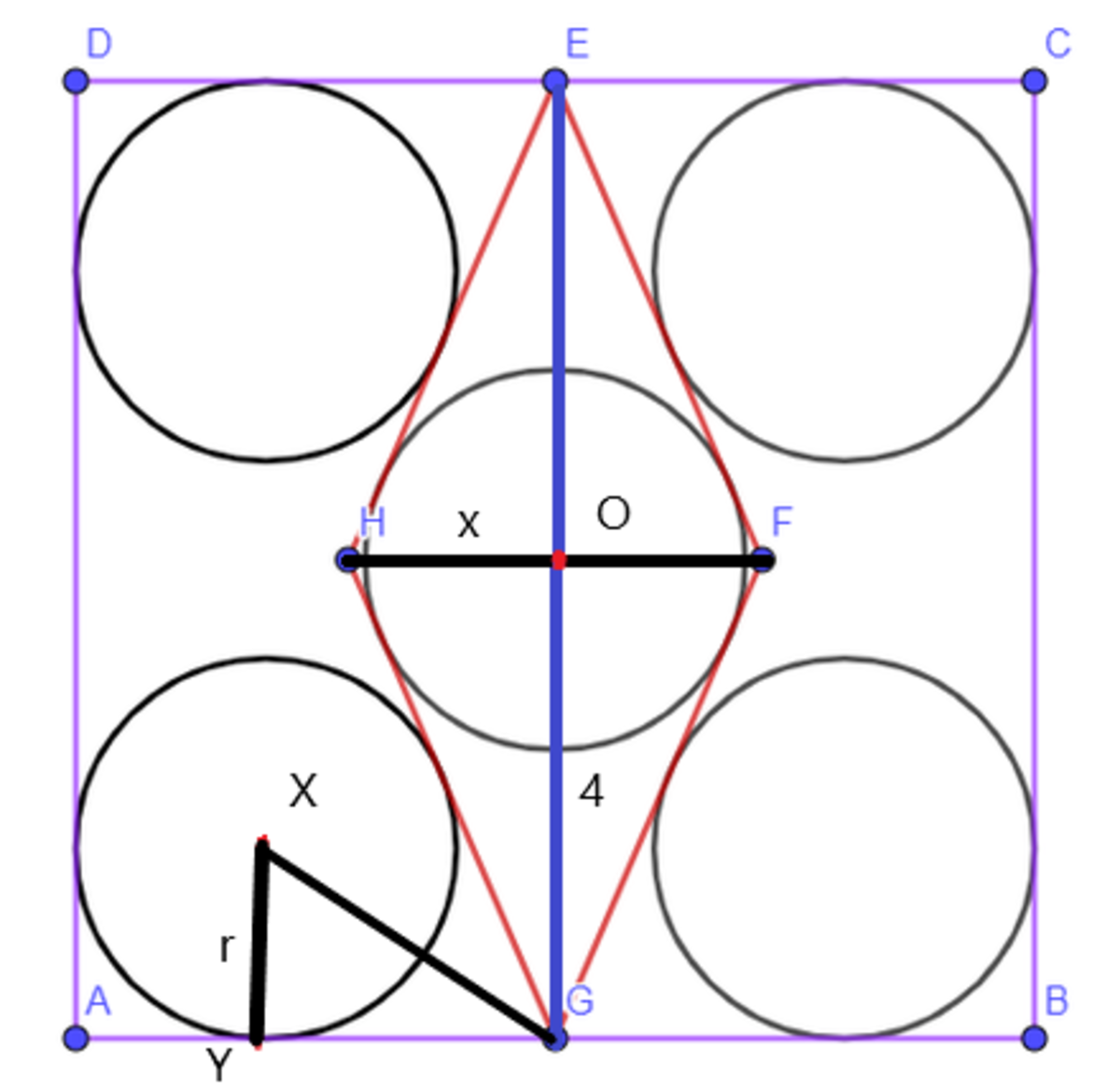
The radius of the incircle of rhombus E H G F is, r = 2 H F 2 + E G 2 H F ⋅ E G = 4 x 2 + 6 4 8 x ( 1 ) Let ∠ H G O = 2 α ⟹ ∠ A G H = 9 0 ∘ − 2 α . Since the center of the incircle ( X ) lies on the angle bisector of ∠ A G H , ∠ A G X = ∠ Y G X = 4 5 ∘ − α In △ H O G , tan ∠ H G O = O G H O ⟹ tan ( 2 α ) = 4 x ⟹ 1 − tan 2 α 2 tan α = 4 x ( 2 ) In △ X Y G , tan ∠ Y G X = Y G X Y ⟹ tan ( 4 5 ∘ − α ) = 4 − r r ⟹ 1 + tan α 1 − tan α = 4 − r r Solving for tan α in the above equation, tan α = 1 + 4 − r r 1 − 4 − r r = 1 − 2 r Substituting this in ( 2 ) , 1 − tan 2 α 2 tan α = r − 4 r 2 2 − r = 4 x ⟹ x = 4 r − r 2 3 2 − 1 6 r Substituting this in ( 1 ) , r 2 = 4 x 2 + 6 4 6 4 x 2 = 4 ( 4 r − r 2 3 2 − 1 6 r ) 2 + 6 4 6 4 ( 4 r − r 2 3 2 − 1 6 r ) 2 Solving this equation in r ,we have, the radius of the five circles is r ≈ 1 . 5 8 6
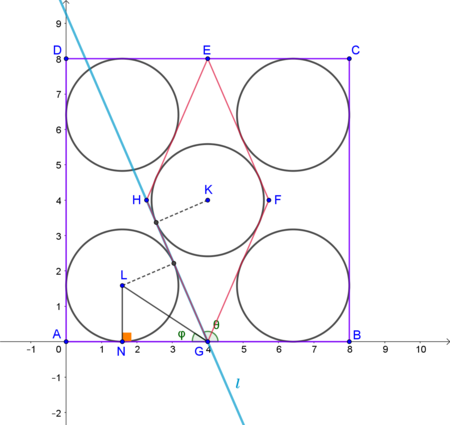 As seen in the figure, we place the square on a coordinate plane. Point
A
is on the origin and point
B
lies on the positive x-semiaxis, i.e.
B
(
8
,
0
)
. The center of the rhombus’ incircle is
K
(
4
,
4
)
and the center of the lower-left circle is
L
(
r
,
r
)
, where
r
is the radius of the circles.
As seen in the figure, we place the square on a coordinate plane. Point
A
is on the origin and point
B
lies on the positive x-semiaxis, i.e.
B
(
8
,
0
)
. The center of the rhombus’ incircle is
K
(
4
,
4
)
and the center of the lower-left circle is
L
(
r
,
r
)
, where
r
is the radius of the circles.
L
N
is perpendicular to
A
B
. Let
θ
=
∠
B
G
H
and
φ
=
∠
L
G
N
. Then,
tan 2 θ = cot ( 2 π − θ ) = cot φ = L N N G = r 4 − r ( 1 ) The line l through points G and H has equation y = m ( x − 4 ) ⇔ m x − y − 4 m = 0 , where m is the slope of l . Thus,
m = tan θ = 1 − tan 2 2 θ 2 tan 2 θ = ( 1 ) 1 − ( r 4 − r ) 2 2 r 4 − r ⇒ m = 4 r − 8 4 r − r 2 ( 2 )
l is tangent to both circles with centers K and L , hence these two points are equidistant from l . Using the distance formula found here we have
m 2 + 1 ∣ m r − r − 4 m ∣ = m 2 + 1 ∣ 4 m − 4 − 4 m ∣ ⇔ ∣ m r − r − 4 m ∣ = ∣ 4 m − 4 − 4 m ∣ ⇔ ∣ m ( r − 4 ) − r ∣ = 4 ⇔ m ( r − 4 ) − r = − 4 or m ( r − 4 ) − r = 4 Asume m ( r − 4 ) − r = − 4 . Combining with ( 2 ) ,
4 r − 8 4 r − r 2 ( r − 4 ) − r = − 4 ⇔ … ⇔ r 2 = 8 ⇔ r > 0 r = 2 2 This value is rejected, because, obviously, 4 r < 8 ⇒ r < 2 . Hence, the relation that holds is m ( r − 4 ) − r = 4 . Again, with ( 2 ) ,
4 r − 8 4 r − r 2 ( r − 4 ) − r − 4 = 0 ⇔ … ⇔ r 3 − 4 r 2 + 2 4 r − 3 2 = 0 The unique real solution of this equation gives the answer: r ≈ 1 . 5 8 6 4 .
Label the bottom left as follows, and let r be the radius of one of the circles and let θ = ∠ I G J = ∠ J G K .
Since ∠ I G L is a right angle, ∠ K G L = 9 0 ° − 2 θ , and since ∠ L K G is a right angle, ∠ K L G = 2 θ .
As half the length of the square, A G = G L = 4 , and since A I = r , I G = 4 − r .
By the Pythagorean Theorem on △ I G J , J G = ( 4 − r ) 2 + r 2 = 2 r 2 − 8 r + 1 6 , so that cos θ = 2 r 2 − 8 r + 1 6 4 − r , sin θ = 2 r 2 − 8 r + 1 6 r , and cos 2 θ = cos 2 θ − sin 2 θ = r 2 − 4 r + 8 8 − 4 r .
From △ K L G , cos 2 θ = 4 r .
Therefore, cos 2 θ = r 2 − 4 r + 8 8 − 4 r = 4 r , which rearranges to r 3 − 4 r 2 + 2 4 r − 3 2 = 0 , and solves numerically to r ≈ 1 . 5 8 6 4 .