A square and two rectangles in a round hole
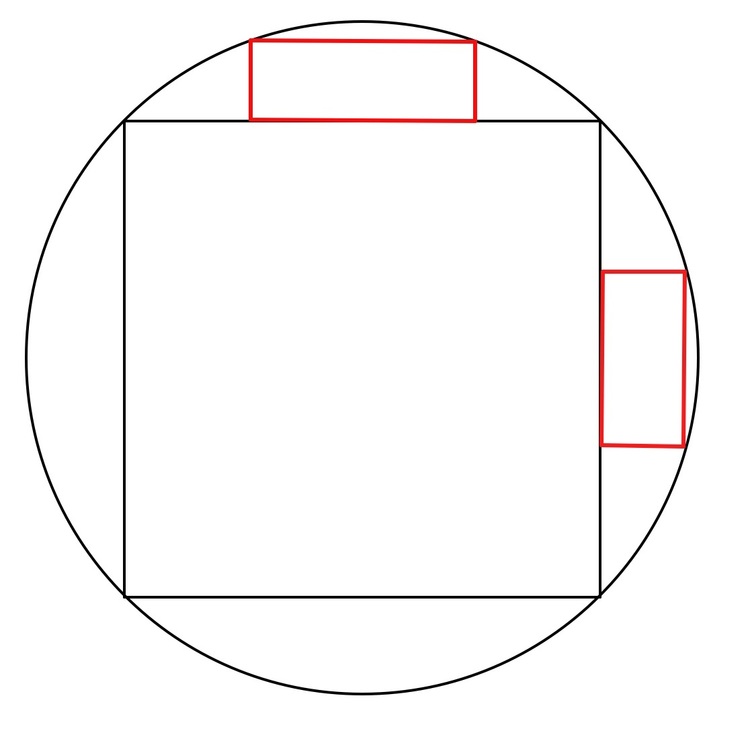 A square section is cut out of a circle as depicted above. Next, two random rectangles which do not overlap with the other rectangle or the square are cut out of the remaining sectors of the circle. If the maximum possible ratio of the cut out area C to the total area of the circle S is
S
C
. Find
A square section is cut out of a circle as depicted above. Next, two random rectangles which do not overlap with the other rectangle or the square are cut out of the remaining sectors of the circle. If the maximum possible ratio of the cut out area C to the total area of the circle S is
S
C
. Find
⌈ ( 1 0 0 0 S C ) ⌉
Note: this problem was inspired by one of Sir Brian Charlesworth: Rectangular Pegs in a Round Hole
Assume:
Use of a computer software for ARITHMETIC is allowed.
⌈ x ⌉ means the least possible integer greater than or equal to x
Exg: ⌈ 4 . 1 ⌉ = 5
The answer is 744.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We'll work assuming that the circle's radius is 1 just to keep our solution pretty.
We begin with making a circle with the equation x 2 + y 2 = 1
The inscribed square has a height of 2 , thus the distance from the center to the top is 2 2 .
To make the top side even with the x axis, we must make a vertical shift of 2 1 units down and our graph becomes
x 2 + ( y + 2 1 ) 2 = 1
⇒ y = 1 − x 2 − 2 1
Now, looking at the rectangle, we see that the base is along x=0, thus the base length will be 2 x (x is the coordinate of the base along the x-axis).
The height y i will be corresponding to x i . Thus using the formula area=base*height, we get A = ( 2 x ) ( 1 − x 2 − 2 1 )
To maximize this, we take the derivative d x d A and set it equal to 0
d x d A = ( 2 x ) ( 1 − x 2 − 2 1 )
We differentiate in parts
0 = ( 2 ) ( 1 − x 2 − 2 1 ) + ( 2 x ) ( 1 − x 2 − x )
Multiplying out the denominator on both sides and some algebraic manipulation yields 8 x 4 − 7 x 2 + 1 = 0
Using the quadratic then square rooting, we get x = ± 4 7 − 1 7
"Wolfing around" a little with our value of x, plugging it into the equation A = ( 2 x ) ( 1 − x 2 − 2 1 ) .
We get the area of one rectangle to be 8 1 ( − 2 1 4 − 2 1 7 + 4 6 − 2 1 7 )
Multiplying this by 2 (there are two rectangles) and adding the area of the cut out square (2 sq units) and finally dividing everything by the area of the circle ( π sq units we get S C = π 4 1 ( − 2 1 4 − 2 1 7 + 4 6 − 2 1 7 ) + 2 ≈ 0 . 7 4 3 8
Therefore ⌈ ( 1 0 0 0 S C ) ⌉ = 7 4 4
Nice question, Sir Trevor. :) You must have posted your solution while I was writing up mine, because when I finished there, lo and behold, was yours. We used pretty much the identical method as well. Sigh.... I guess people will just have to decide which to vote for based on how 'pretty' they look. :)
Log in to reply
Well, you know what they say. Great minds think alike :D. And thats just the beauty of math. When two people do the same thing it's most likely right.
Log in to reply
Haha. Well, we can only hope. It's interesting that this is only about 5.5% less coverage than the maximum found in the other question. Now on to finding the maximum achievable coverage by 4, 5, ....., N rectangles. :)
I'll try to think of a reasonable length solution not using calc tomorrow, not sure if I'll be able to tho, I think calc may be the only way here that doesn't require 45 mins of bashing.
Log in to reply
I think that there may a Lagrange multiplier approach, but I doubt that it will be any shorter. And besides, that would still be calculus. Given the crazy mess of root signs in own solutions, I doubt if there is a tidier method of solving this problem.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
|
Without loss of generality let the circle have radius 1 , making C = π .
Now the diagonal of the square section is a diameter of the circle x 2 + y 2 = 1 and hence has length 2 . The sides of the square thus have length 2 , making its area 2 .
Now let the center of the circle (and square) coincide with the origin of a superimposed x y -grid, with the square symmetric about both the x and y axes. The top side of the square then lies on the line y = 2 1 . We can assume that the red rectangle at the top of the diagram has maximum area when it is symmetric about the y -axis. Letting its right side have horizontal component x > 0 , its area A will be
A = 2 x ∗ ( 1 − x 2 − 2 1 ) .
To find any critical points we then set d x d A = 0 :
d x d A = 2 ∗ ( 1 − x 2 − 2 1 ) + 2 x ∗ ( 1 − x 2 − x ) = 0
⟹ 1 − x 2 − 1 − x 2 x 2 = 2 1
⟹ 1 − x 2 1 − 2 x 2 = 2 1
⟹ 2 ∗ ( 1 − 2 x 2 ) 2 = 1 − x 2 ⟹ 8 x 4 − 7 x 2 + 1 = 0 ,
which is quadratic in x 2 with solutions
x 2 = 1 6 7 ± 1 7 ⟹ x = 4 7 ± 1 7 .
Now note that the coordinates of the top right vertex of the square is ( 2 1 , 2 1 ) , and thus we must have x ≤ 2 1 . Only one of our potential solutions meets this requirement, namely
x = 4 7 − 1 7 .
This gives us the value A = ( 8 7 − 1 7 ) ∗ ( 9 + 1 7 − 2 2 ) .
Given that the minimum possible value for the area of the red rectangle, (ranging over the possible values for x ), is zero, we can surmise that the value for A found above is a maximum. By symmetry, the red rectangle on the right side of the square has the same maximum area value. The maximum possible ratio of the cut-out area to the area of the circle is then
S C = π 2 + 2 A = 0 . 7 4 3 8 1 0 6 . . . . , making ⌈ 1 0 0 0 ∗ S C ⌉ = 7 4 4 .