A square frame projected towards an infinite current carrying wire.
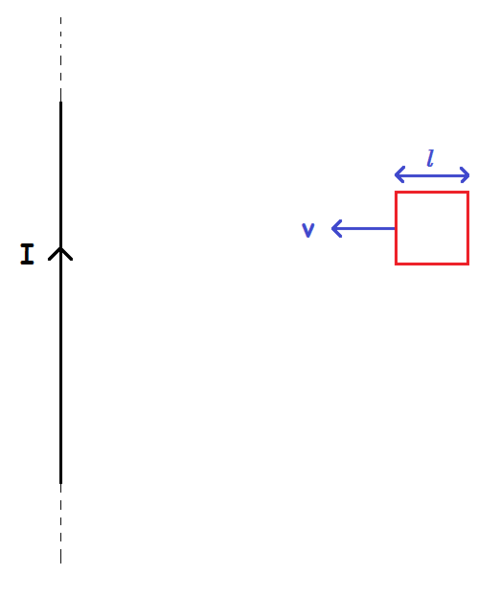 A square frame of length
m, mass
g, resistance
is projected from a large distance towards a fixed infinitely long wire carrying current
kAmp with a speed
m/s.
A square frame of length
m, mass
g, resistance
is projected from a large distance towards a fixed infinitely long wire carrying current
kAmp with a speed
m/s.
Let be the total distance of the left part of frame from wire in metres when the frame comes to rest.
Find
The answer is 250000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The magnetic flux through the square frame when the left part is at a distance x from wire is ϕ = ∫ B d A = ∫ 0 l 2 π r μ 0 I l d r = 2 π μ 0 I l ln ( 1 + x l )
Now, the induced emf is ∣ ϵ ∣ = ∣ ∣ ∣ ∣ d t d ϕ ∣ ∣ ∣ ∣ = − 2 π x ( l + x ) μ 0 I v (Note that v = d t d x is -ve)
Now, the induced anticlockwise current is i = R ∣ ϵ ∣ = − 2 π R x ( l + x ) μ 0 I v
Net force experienced = F = 2 π μ 0 I i ( x 1 − l + x 1 )
= − ( 2 π x ( l + x ) μ 0 I l ) 2 R v
⇒ m d x v d v = − ( 2 π x ( l + x ) μ 0 I l ) 2 R v
∫ ∞ a ( x ( l + x ) ) 2 d x = − ( μ 0 I l 2 π ) 2 m R ∫ − v 0 0 d v
Since, l = 1 m , we get ∫ a ∞ ( x ( 1 + x ) ) 2 d x = 2 5 0 0 0 0 m − 3