A Square In A Dodecagon

The area of a regular polygon with $n$ sides inscribed in a circle of radius $R$ is $A = \frac{nR^2}{2} \sin (\frac{360}{n})$ , which means the area of a regular dodecagon (when $n = 12$ ) is $A = 3R^2$ and the area of a square (when $n = 4$ ) inscribed in the same circle is $A = 2R^2$ . The ratio between the area of a square and the area of a dodecagon inscribed in the same circle is therefore $\frac{2}{3}$ , so the area of the above square can be found by solving the proportion $\frac{x}{12} = \frac{2}{3}$ , which is $\boxed{8}$ .

---

The picture below shows that the ratio between the area of the square inscribed in a regular dodecagon in this way is $\frac{2}{3}$ the area of the regular dodecagon:

where each smaller triangle or quadrilateral of the same color are congruent, and can be rearranged to form the following large triangle found in the square,
and rearranged again to form the following large triangle found in the regular dodecagon:

at the following side ratios and angles:

NOTE: In case, you are not aware of the formula $\frac{nR^2}{2}\sin(\frac{360^\circ}{n})$ , then the method below will help you.

Let the side of the polygon = $a$ units

Let the apothem of the polygon = $b$ units

We observe that the side of a square = $2a\cos30^{o}$ + $a$ = $(\sqrt3 + 1)$ $a$ ... (i)

Since the polygon is regular, we can find the angles subtended at various positions as shown. Use the $\frac{(n-2)180^{o}}{n}$ formula to find the internal angles subtended by the sides, where n is the number of sides of the regular polygon. To find the angle at the centre made by the triangle, simply divide $\frac{360}{n}$ . The regularity allows for the angles to be bisected. The values thus obtained are in the figure above.

Area of any polygon = $\frac{1}{2}$ x apothem x perimeter = $\frac{1}{2}$ x $b$ x $12a$ = $6ab$

$\implies$ $12$ = $6ab$

$\implies$ $ab$ = $2$ ... (ii)

Now to find $b$ , we make the triangle as shown in the figure.

$b$ = $\frac{a}{2}$ x $\tan75^{o}$ = $\frac{a(\sqrt3 + 1)}{2(\sqrt3 - 1)}$ ... (iii)

Putting (iii) in (ii);

$\frac{a^{2}(\sqrt3 + 1)}{2(\sqrt3 -1)}$ = 2

$\implies$ $a^{2}$ = $\frac{4(\sqrt3 - 1)}{\sqrt3 + 1}$ ... (iv)

Area of Square from (i) = $a^{2}(\sqrt3+1)^{2}$

Using (iv):

Area of Square = $\frac{4(\sqrt3-1)}{\sqrt3+1}$ x $(\sqrt3+1)^{2}$ = $4(3-1)$ = $8$ square units

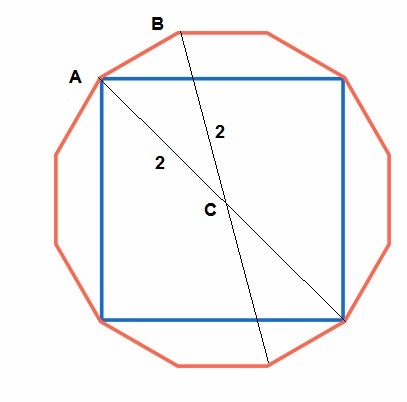Total area = 12 = 12 x Area of $\triangle ABC \implies$ Area of $\triangle ABC = 1$

Area of $\triangle ABC = \dfrac {AC \times BC \ \sin 30 }{2} = 1 \implies AC = BC = 2$

The diagonal of the given square = 4 and the Square area = 8;