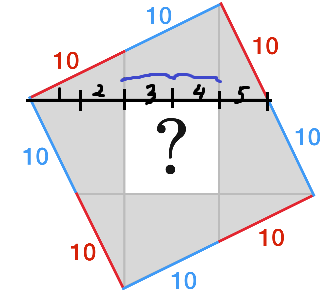
A Square Inside A Square!
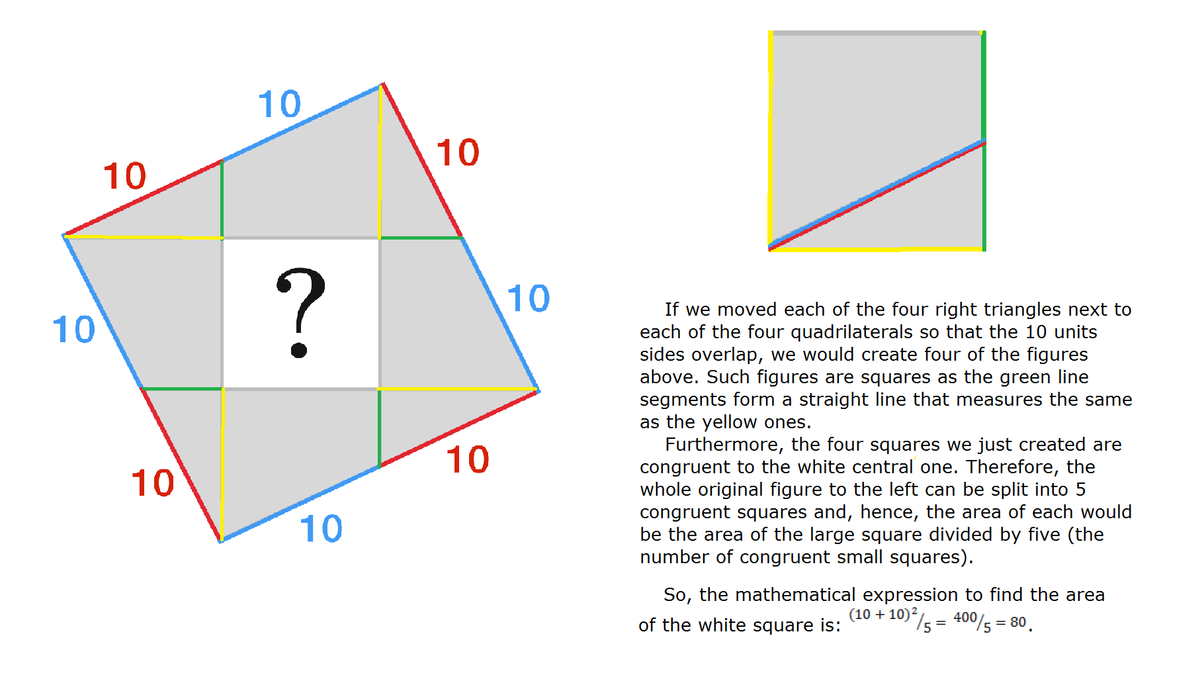
Line segments are drawn from the vertices of the large square to the midpoints of the opposite sides to form a smaller, white square.
If each red or blue line-segment measures 1 0 m long, what is the area of the smaller, white square in m 2 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
41 solutions
Beautiful!
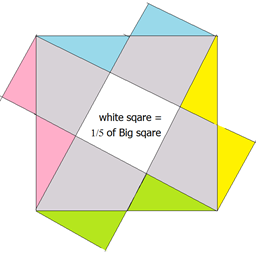
I was sure you were wrong. I took a brain lock and assumed a 3 , 4 ,5 right triangle ( don't know where this came from ) and then proceeded to work out the dimensions of the smaller triangles. It wasn't until I was trying to establish that the boxes were the same that I discovered my error and wondered where my head was when I said 3, 4, 5. I knew something was wrong because I got areas that did not agree ,when I approached it from a different perspective . Nothing makes you focus like a wrong assumption and laboriously trying to make the solution fit your assumption
How do you know they are divided into squares of equal parts? I thought those other squares are bigger than the white square
Log in to reply
Think of the line from the corner to the opposite side as the X axis, then the side of the square is f (x). Since the side of the square is straight f (x) is a constant function, then since it increased 10 after some X and some Y, then another 10 show's another X and Y. So the length all squares are X. And Y= 1/2 X.
Well, I just draw some paralles lines and so on!
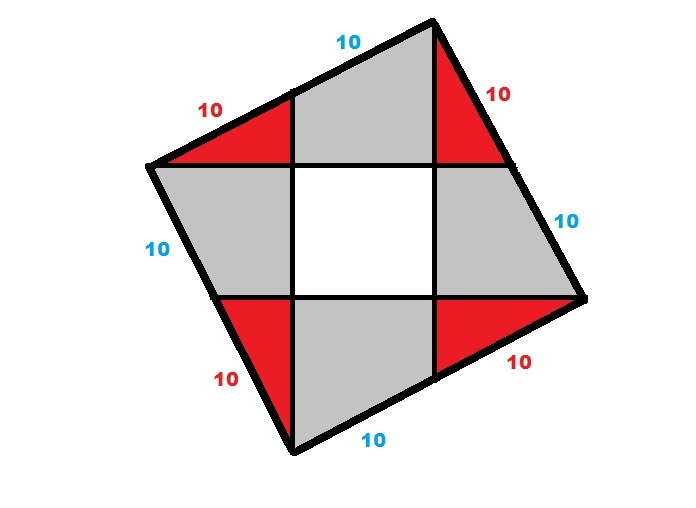
Total area: 20 triangles.
Yellow zone: 4 triangles.
(20 cm x 20 cm) / 20 triagles * 4 triangles = 80
I find this the most 'transparent' solution. One general way to solve such problems is to look for the smallest 'unit' of area (the tiny triangle) and count using those.
Log in to reply
This looks good if you can prove that all triangles are congruent. I haven't been able to do that, and I think it's needed to verify you proof.
I guess I thought the red segments could be seen as the hypotenuse of right triangles with sides of 6 and 8 by the Pythagorean Theorem (PT). Again by PT, a triangle with sides of a red+blue (20) and a red side (10) would have an hypotenuse of the square root of (20^2 + 10^2) = 22.63. Subtracting 8 and 6 from that gives a side of the inner square of 8.36 and squaring that is 69.9 --> not an answer! Which means my assumption about the triangles (green, pink, blue and yellow) are not right triangles was incorrect. However, the way they're used in the solution indicate they ARE right triangles so I'm confused.
Log in to reply
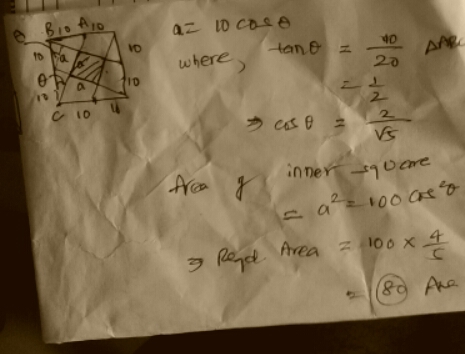
All of the triangles in the diagram are Right Triangles. To use PT which I did, First you must fined the hypotenuse of one of the large triangles made by 2 corners and an adjacent midpoint. A is 20 B is 10 so 100 + 400 = 500. Get the square root of 500 and you have the length of the H is 10 sqrt(5). Then to figure out the height of the small triangles well since the angles are the same you know they are similar to this larger triangle. so you know that the hyp of a smaller triangle is 10 you can then figure out the ratio of the large triangle to the small triangle is 10/sqrt(5) then by PT you know that c^2 - b^2 = a^2. a^2 is equivalent to a side of the square. 100 - (10/sqrt(5))^2 = b^2 100 - 100/5 = b^2 100 - 20 = 80. since the area of the square is b^2 the answer is 80.
You made an incorrect assumption that the small triangles had sides of 6 and 8. Although the 6, 8, 10 triangle is a possible and well-known triangle, it is not the only possibility for side-lengths. In this case, the lengths are 5 1 0 and 5 2 0 with a hypotenuse of 10.
Your method is damn cool
If we move the 4 triangles to complete the 4 blue squares , we see that the area of the big square gets divided into 5 equal parts(squares).
Hence area = 5 2 0 2 = 5 4 0 0 = 8 0
i have a doubt that , always a square has an area , a no. which is a perfect square. but in the question u mentioned that the smaller white quadrilateral is a square and in the options the only perfect square was 100 , but your ans. is 80, which is not a perfect square. plz clarify .
Log in to reply
Mrunang, that is because no one said that the whole area would be the sum of squares of INTEGER values... the side came out to be 20 x root(2)...
Short cut is good.i have arrived at same as by assuming radii of four circles/semicircle are R;R/2;R/3 ;R/6.subtract from area of quadrat which are inside quadrant we get same 80 as answer .iI have a picture to derive but don't know how to post written answers here.
How can you prove they divided into equal parts?
@Chung Kevin Reminds me of your colorful problems!
Log in to reply
Thanks! I like this problem too! I've seen it before, and the trick of 5 equal parts is really beautiful.
you are good i wantto talk to you send me your facebook id
can u please explain in the drawing?
Log in to reply
ok I get it now, but mathematical figures should be more appealing I guess, perticularly in forming the blue square
if each red line and blue =10 then all sides would be 20m my bad i missed your square so then the answer is 10 square
I think you need to say something about why moving the triangles would form squares, not just rectangles.
Pythagorean theorem = a^2 + b^2 = c^2 if c = hypotenuse for triangle made up of 1 side of large square and half of other side = c^2 = 20^2 + 10^2 = 500^2 (square route for c) Area of square in question is (c x 40%)^2 (c = 2/5 times length of small square side) 8.944...^2 = 80 (area of small square is 80m squared)
I think since the side is a straight line and since the line from the vertices cut the opposite side in the middle, the middle line can be the X axis, and the side of the square a constant increase. Since the side length becomes 10 after X distance it must increase some height Y then another 10 implies another X and Y. There fore 2Y=X. The irregular peice in the middle is a square of height and width X but is missing a triangle of height 1/2 X and width X. Since there are 4 of these shapes with 4 little triangles the can be grouped to form 5 squares with side length X, Total area of 400, therefore each Square must be 80.
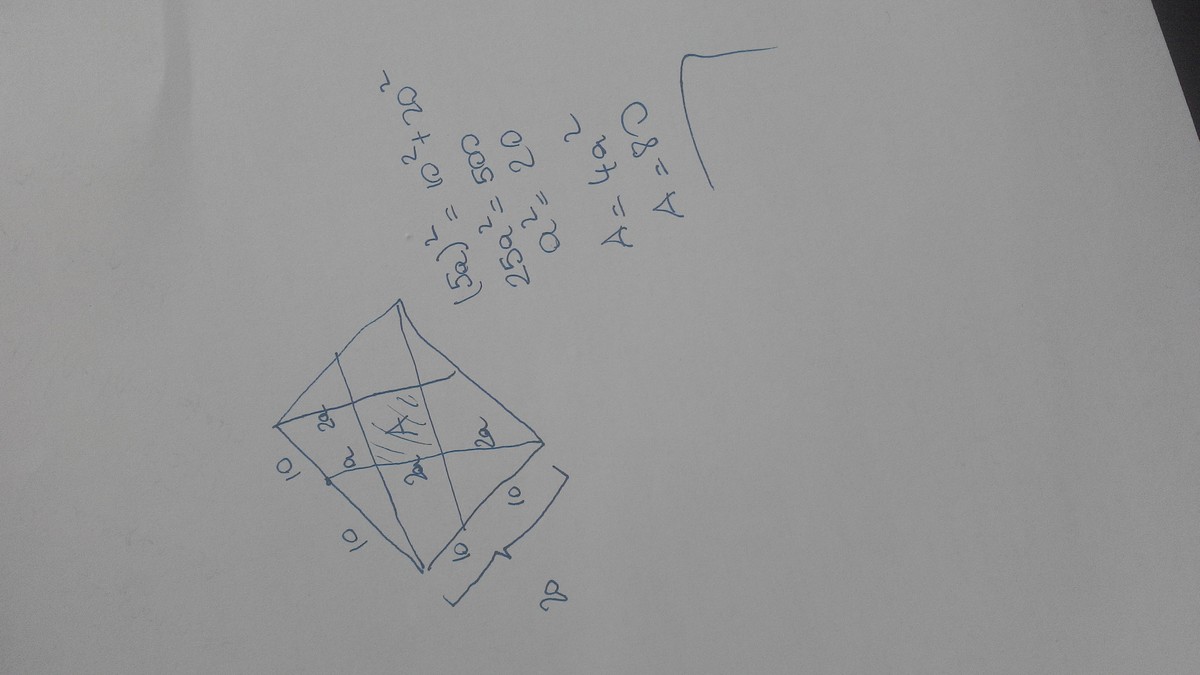 See the pic above
See the pic above
Forget about memorizing any theory, all you need is creativity
Mr. ozturg, this is absolutely a correct approach, but how do you prove that the ratio of lenghts which u have considered in the image is correct????
Log in to reply
You can prove that using similar triangles.
Quite elementary; Rules for triangles in Archimedes geometry if we draw a straight line that cuts two sides of the triangle and is parallel to the third side. then the new triangle is proportionate to the original triangle.
If the line cuts the two sides in the middle; the new triangle is half of the original (ie: lines facing the same parallel angles are half the original length
I solved it the same way you did.
I used the old SOHCAHTOA rule I memorized in high school. In a right triangle, take one of the corner acute angles, and the lengths of the known sides, SOH, the Sine of either acute angle is equal it's Opposite side length divided by the Hypotenuse length, CAH, Cosine of an acute angle is equal the Adjacent side divided by Hypotenuse, and TOA, Tangent of acute angle is equal it's Opposite side divided by it's Adjacent side.
From there you can calculate the larger acute angle (A) of the 10x20 triangle, Tan(A) = Opp / Adj Tan(A) = 20 / 10... (A) = Arc Tan (2) 63.43494.....
Given the angle (A) you can calculate the length (L) of the side of the middle square based on half the length of the large square,
Sin(A) = Opp / Hyp
Sin (A) = (L) / 10
(L) = 10 x Sin(A)
8.94427.....
Area of the smaller square is now simply (L) ^2... Area = (L) x (L) 80.
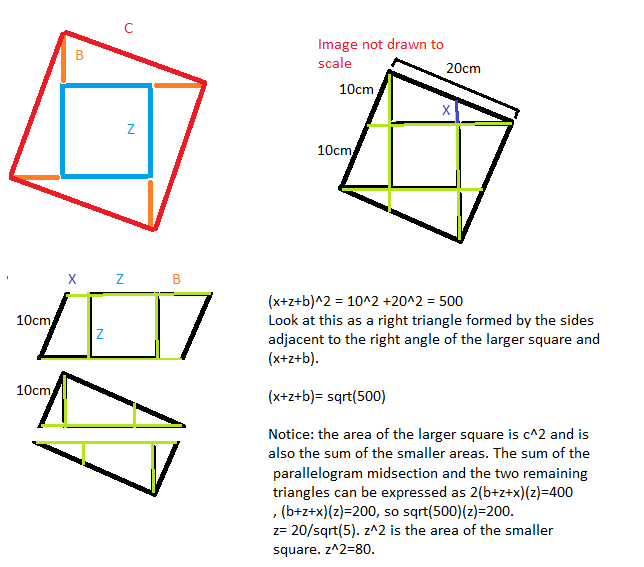 Z^2 = 80. It is possible to solve for the individual areas that fill this large square.
Z^2 = 80. It is possible to solve for the individual areas that fill this large square.
The slant line by Pythagoras is 1 0 5 . The slant line is clearly decided into 2.5 parts out of which the side of yellow square is 1 part= 4 5 . So the yellow area = 80.
Using a word like "clearly" to judge distances is anathema to a geometry proof.
Log in to reply
No it is clearly. Because a hypotenuse that is double a leg is a 30 60 90 triangle.
The white square is middle part of a parallelogram of which base length is 10 and height is 20, and therefore area is 10×20=200. The side of white square constitutes 2 parts out of 5 parts length of the slant side of parallelogram, because the slant side is composed of 3 pieces of which 2 are of same length being projections of equal parts of a straight line and the third piece is of half length being the other side of the triangle which is similar to the triangle having sides 10, 20 and the slant side of the parallelogram. Therefore, area of white square is 2/5th of parallelogram area and is 200×2/5=80.
Best answer by far. Elegant and fast! Thanks.
My approach on this one was to place the square on a coordinate plane such that the axes are at 0,0; 20,0; 0,20; and 20,20. The inner lines are defined then as: y1 = -1/2x + 10 y2 = 2x y3 = 2x - 20 y4 = -1/2x + 20
We just need one side of the square, which just needs the intersection of y1 and y2 along with the intersection of y1 and y3.
These intersections are at 4,8 and 12,4. Consider a right triangle with its hypotenuse running between those two points. Its other two sides would be 4 and 8. 4^2 + 8^2 = 80. sqrt(80) is thus the length of one side of the inner square. Square it and you arrive at 80.
I prefer the analytic geometry approach here.
Oh, and you could use the original version of the Pythagorean theorem, which refers not to squares of distances, but areas of squares formed by the various sides of the right triangles. That would save you the trouble of taking the square root of a number, only to re-square it immediately.
Very Nice! You re-introduced the amazing power of analytic geometry. Incredible how you simplified the whole problem by rotating the big square onto your re-oriented coordinate plane. "The simplifying consequences of a favorable choice of coordinate system" ---amazes me every time! :-)
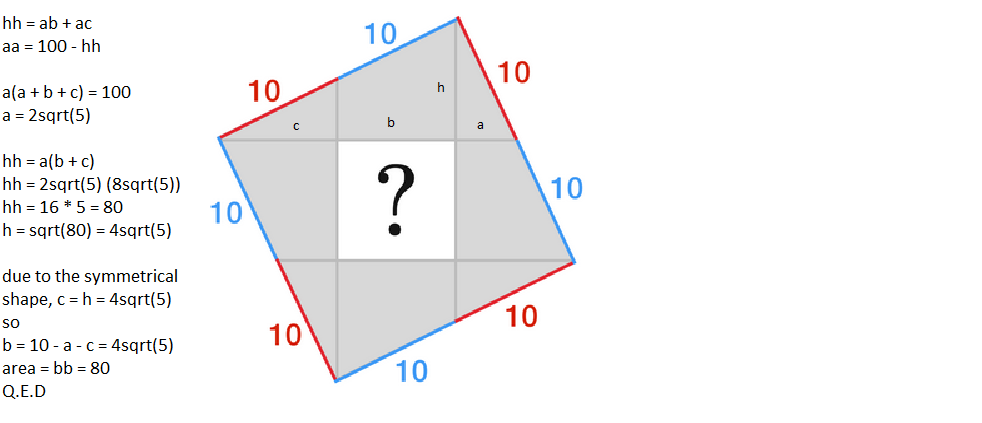
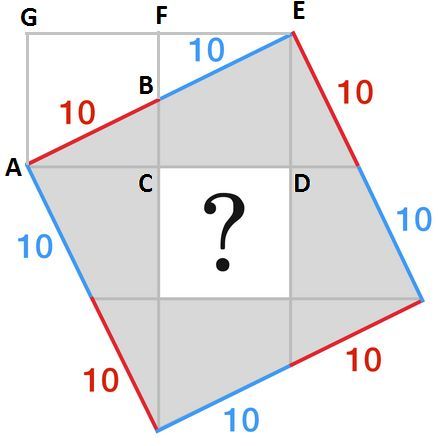
In the expanded figure below, based on proportionality, we have AC = CD = DE = EF = FC and BC = FC/2 = AC/2.
In the triangle ABC, AB^2 = AC^2 + BC^2. Replacing BC by AC/2 and AB by 10: 100 = AC^2 + AC^2/4. Multipling both mebers of the equation by 4: 400 = 4
AC^2 + AC^2 = 5
AC^2, from which AC^2 =
80
. This is also the area of the inside square.
Area of two right angled triangles of base 10 height 20 is 200
Area of two trapeziums and inner square must be 200
Let length of square is x
(10√5-x)*x+(x^2)=200
solving equation gets x
area is x*x=80
If we move the 4 triangles to complete the 4 blue squares.there for total squares are 5.Area of big squre is 400 cm square.hence 400/5=80.80cmsquare is the correct ans.
Place the small triangles with the red line segments on the blue line segments of the trapezoids. You will find a cross of 5 equal squares. So, the white square is 5 1 of the entire area. 5 ( 1 0 + 1 0 ) 2 = 5 2 0 2 = 5 4 0 0 = 8 0
There is probably a faster way using a solution similar to this, yet I found this semi intuition quite interesting
The large right triangles formed that have a base of 20 and a height of 10 will have a hypotenuse of 10√5. The small right triangles that have a hypotenuse of 10 are similar to the large right triangles since they coincide at one right angle and also each have a right angle. Therefore, the short leg to hypotenuse ratio should be the same in both the small and large triangles, thus 1 0 x = 1 0 √ 5 1 0 and x = 2√5 which is the length of the short leg in the small triangle. Using the Pythagorean Theorem, the long leg of the small triangles is 4√5, which then creates segments of length 2√5, 4√5, and 4√5 along the hypotenuse of the large right triangles. The center hypotenuse section of 4√5 is the length of the side of the center square, so the area of that square is 4√5 • 4√5, which equals 80.
? = ( 5 2 0 2 + 1 0 2 × 2 ) 2
Only problem is the question states that the edges are 10m, making the total area 100m2, and the area of the white square 20m2...
we could solve for the side of the square, but first we should solve for the angle formed by each triangle.
For a smart solution. Use similar triangles, there aren't any labels so it's hard to describe, but if you use pythagoras you find the length of one of those diagonals is 10sqrt5. and some triangles are similar so you find that 10sqrt5/20 = 20/somelength Now, from another pair of similar triangles, somelength is double the length of the square by AA congruency with the ratio of 1/2. Thus the length of the square is somelength/2. And you will find somelength = 40/sqrt5, so somelength/2 = 20/sqrt5=4sqrt5. So the square is 16*5=80.
For a less smart solution use coordinate geometry and use the distance formula to find the length of a side of the square after finding the intersections.
Using the smaller triangles (with a red line as an hypotenuse) it is possible to fold them over to create 5 equal squares (The square with the ?, and 4 other congruent squares). Thus the square with the "?" is 1/5 the total area.
With this in mind: Find the total area; 20 * 20 then divide by 5 for the answer: 80
We know that the line segments are drawn from each corner to the midpoint of the opposite side. We also know that the internal angles of every square are equal to 90 degrees. As a result, 4 equal right triangles are formed. Using the pythagorean theorem, we find that the hypotenuse of each right triangle is equal to the square root of 500, which is equal to 10 times the square root of 5. We notice that the hypotenuse of this triangle consists of each side of the smaller square except for its hypotenuse and one side of the smaller square.
We see that the smaller triangles are formed with a hypotenuse of 10 m each. As they are all equal, lets consider one of them. To calculate the size of its perpendicular sides we must compare it to the bigger triangle. We find that the triangles are similar as they are both right triangles (the smaller one is right due to the fact that one of its angles is opposite to the 90 degree angle of the smaller square) and they share one acute angle.
We know the hypotenuses of the bigger and smaller triangle and the side of the bigger triangle which is equal to the side of the bigger square. Using algebra, we find that the similar side of the smaller triangle is equal to 4 times the square root of 5, which is roughly equal to 8.9 m. The smaller side is then roughly equal to 4.5 m.
Taking the hypotenuse of the bigger triangle, we subtract the two perpendicular sides of the smaller triangle to find the side of the smaller square. It is roughly equal to 8.9 m. By squaring the number we can find the area of the smaller square. It is equal to 79.21 ~ 80.
The square is 400. Each large triangle is 100. Add two that do not overlap (eg left and right) gives 200. Therefore the quadrilateral that forms the centre section is also 200. The hypotenuse of each triangle is 1 0 5 . The area of that quadrilateral is 1 0 5 × x where x is one side of the square. So 1 0 5 × x = 2 0 0 giving x = s q r t 5 2 0 and the area of the square is x 2 or 80.
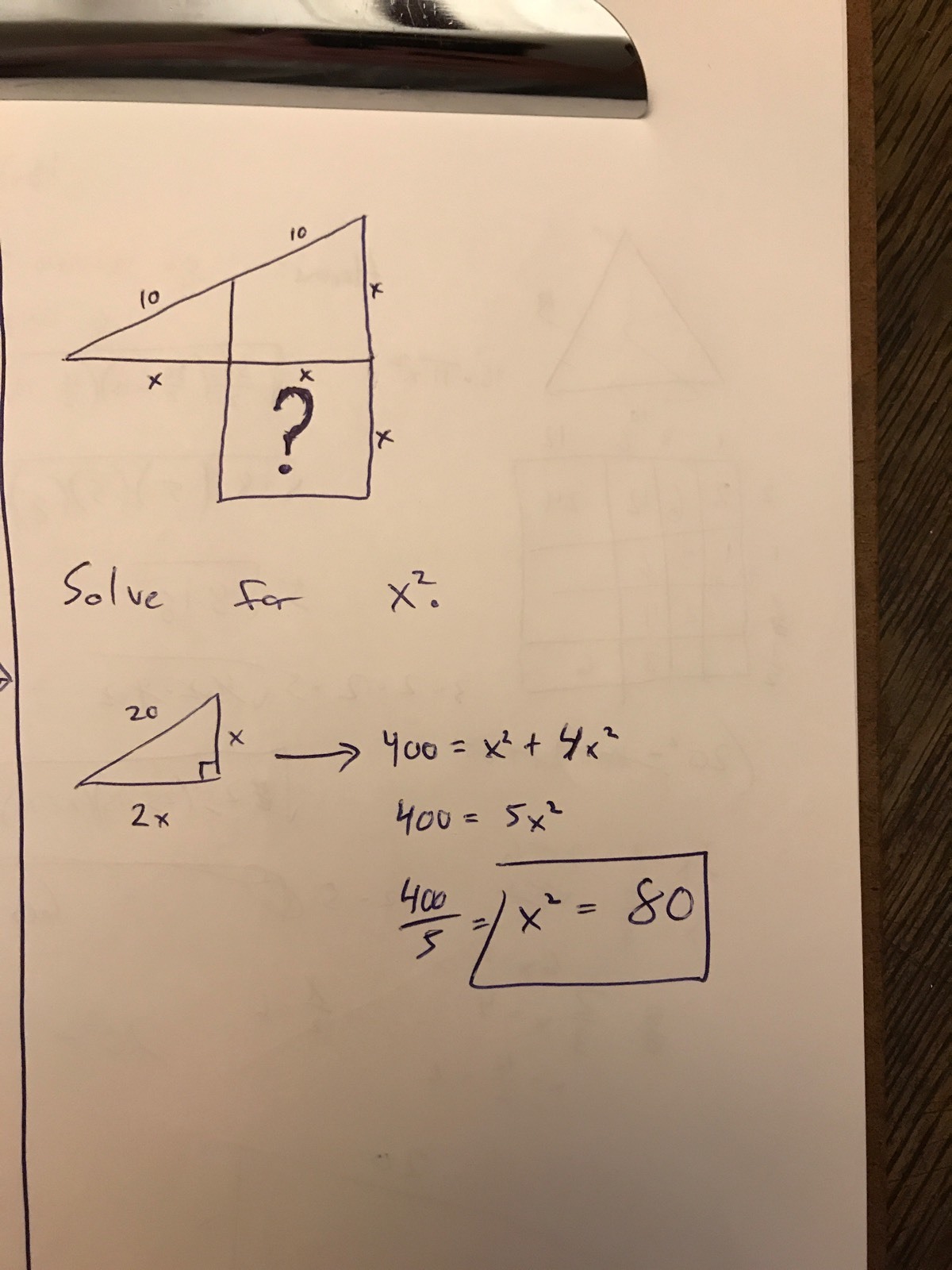
Calling the side length of the white square x, and joining the small triangles with the trapeziums give us the equation 4 x 2 + x 2 = 2 0 2 . Putting this together gives us 5 x 2 = 4 0 0 . Dividing through by 5 gives us x 2 = 8 0 .
Realizing the grey parts with the blue edge and the red edge can be put together with the coloured edge to create a square of the same size as the white one is key. But how do we prove it's true?
First, do they really snap together perfectly? Going along the edge of the big square from red to blue that's a straight line (180°). It's composed of two angles between the red and grey line and the grey and blue line. Hence rotating one piece around the point where the grey, red and blue line meet until the red and blue snap together, that's still 180°, the edge is straight.
Second are both of the edges of what can still be a rectangle the same length as that of the white square? One of them is easy, it directly connects to the white square, so it has to be the same length. Let's say side a .
The other one, side b , is trickier, you can calculate it, but visually it can be done like so:
b is equal to the longer leg of the red-hypotenuse right angle triangle. Now, look at the right angle triangle whose hypotenuse is the red and blue segments together. It's similar to (a scaled version of) the red-hypotenuse triangle, because the angles are all the same (one of them is exactly identical, one is a right angle, third must be same to add up to 180°). But the hypotenuse is 20 instead of 10 so it is twice as big. So its longer leg is also twice as big. But it's composed of the longer leg of the small triangle and the white square edge.
I. e 2 b = b + a , which means a = b
there is a real long mathematical way which I went: let a be the (smaller)acute angle in the diagram. the bigger acute angle is then Pi/4-a. but that doesnt matter since I'll only use a.
anyways we see that tan(a)=10/20=0.5
aka a=arctan(0.5)
we also see that the small triangles have the same angle a. be x the longer unknown side of such a triangle then cos(a)=x/10 therefor x=10 cos(a)=10 cos(arctan(0.5))
Just draw in some lines parallel to the lines already given, such that these new lines cut the side middle points of the rectangl. you know what I mean. so we see that there this divides the whole field into these small triangles and some rectangles where the rectangles are the length of the suare times 1/2 the length of the square.
anyways, for geomatry reasons the x side of the triangles that we found is the same length as the square side.
therefor the squares area is (10*cos(arctan(0.5)))^2
google says that this equals 80.
I'll leave it up to other people to prove that
So, here's how I did it.
First, i'll provide you with this picture to make my explanation clearer:
Essentially, I just made some areas that were gray before now be red. Specifically, the small triangles.
So we have
r
e
d
triangles,
g
r
a
y
trapezoids and a white square in the middle. 2
r
e
d
triangles and a
g
r
a
y
trapezoid make a triangle, one of these:
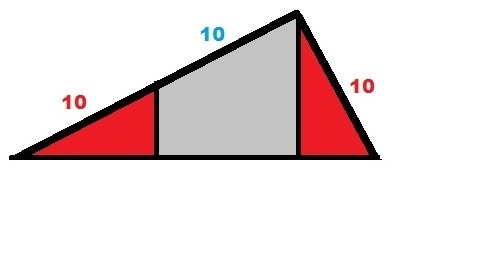 with base
10
and height
20
, and thus a total area of
100
.
with base
10
and height
20
, and thus a total area of
100
.
Now, 1
r
e
d
triangle and a
g
r
a
y
trapezoid, make one of these triangles:
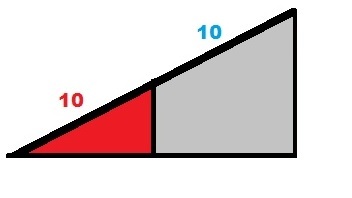 Due to triangle similarity, confirmed via their right sides being parallel, it can be easily seen that this "
r
e
d
−
g
r
a
y
" triangle has
4x the area
of the small
r
e
d
one. This means that the large "
r
e
d
−
g
r
a
y
−
r
e
d
triangles. which we established above have an area of
100
, must each be exactly
5x as large
as the small
r
e
d
triangles. In other words: each of the
r
e
d
triangles has an area of
20
.
Due to triangle similarity, confirmed via their right sides being parallel, it can be easily seen that this "
r
e
d
−
g
r
a
y
" triangle has
4x the area
of the small
r
e
d
one. This means that the large "
r
e
d
−
g
r
a
y
−
r
e
d
triangles. which we established above have an area of
100
, must each be exactly
5x as large
as the small
r
e
d
triangles. In other words: each of the
r
e
d
triangles has an area of
20
.
That, in turn, means that the r e d − g r a y triangles each have an area of 80 . There are 4 of those in the larger square, and subtracting all 4 leaves us with the white square in the middle. So: ( 2 0 × 2 0 ) − ( 4 × 8 0 ) = 4 0 0 − 3 2 0 = 8 0
Note that the hypotenuse of a right triangle with legs 1 0 and 2 0 units is 1 0 5 . Using similar triangles and calling the side length of the square x , we can get that 2 5 + x + 4 5 = 1 0 5 by looking at the hypotenuse of that triangle. Solving this gives x = 4 5 and x 2 = 8 0 .
20 cos@ -10 (sin@ + cos@) where @ is arctan(10/20)
Note that the side of the triangles are x and 1/2x. Set them equal to 10², with pythagoras. 1/4x²+x²=100 Solve for x, hence x= 4 sqrt(5) For the area of the square, we need to square x= 16*5 = 80
As all triangles formed are right angled triangles. So, from underneath triangle 20² + 10² = x² x = √500 As segment contains 2 full sides (imagining all to be squares) and a half side. So, length of each segment y = √500/2.5 This is the length of one side of white square Now area of white square is √500/2.5 × √500/2.5 = 80
Since the gray lines form a white square, we know they are parallel and intersect at 90 degree angles.
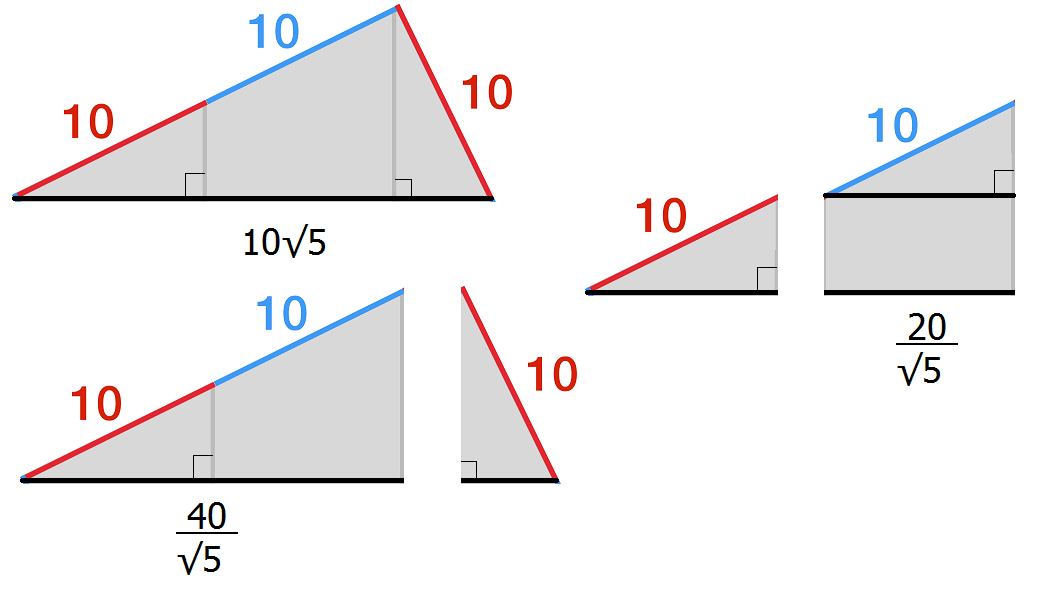 That means the parallel line on the right of the top triangle forms the height of the triangle.
Because that line is the height, we can divide the triangle into two smaller triangles that are similar.
We then know the parallel line on the left is at the midpoint of the larger of the two similar triangles.
This gives us the length of one of the white square's sides = 20√5. Thus,
20√5 squared = 400/5 = 80
That means the parallel line on the right of the top triangle forms the height of the triangle.
Because that line is the height, we can divide the triangle into two smaller triangles that are similar.
We then know the parallel line on the left is at the midpoint of the larger of the two similar triangles.
This gives us the length of one of the white square's sides = 20√5. Thus,
20√5 squared = 400/5 = 80
Area of Exterior ⃞ = 20*20 = 400
◣s with base = 20 and alt = 10 have areas = 20*10/2 = 100
Hypotenuse of such ◣s = √(20^2 + 10^2) = 10 √5
Area of ▱ bounded by two ◣s = 400 - 2(100) = 200
Base of ▱ = 10 √5
Alt of ▱ = 200 ÷ 10 √5 = 20 ÷ √5 = side of Interior ⃞
Area of Interior ⃞ = (20/√5)^2 = 80
Just a quick question. How do we know that the vertices of the large square coincide with the some of the vertices of the smaller squares? I can see that this is the case intuitively but is there any way to prove it?
all triangles are similar
say a is the small angle, tan(a)=10/20=1/2 so a is 0.4635 rad
side square / blue (or red) line is cos(0.4635)= 0.89443
white square side is 10m x 0.89443, so white square area is 8.9443² = 80 m²
How did you assume it to be 5 equal parts? I went so hard ways to solve it... !!
area of the small square = area of large square - 4(area of the large triangle) + 4(area of the small triangle)
*area of the large square=400 sq.cm. *area of the large triangle=100 sq. cm.
since the small and large triangle is similar, then their sides must be on the same ratio. ( one leg is twice the other leg)
Area=1/2(x)(2x)=x^2 using pythagorean theorem ;(10)^2 = (x)^2 + (2x)^2 we get : x^2 = 20 therefore;
*area of the small triangle=20sq. cm.
then substitute all the values to the 1st equation we get; Asmallsq. = 400 sq.cm. -4(100sq.cm.)+4(20sq.cm)
final answer ; Asmallsq = 80 sq.cm.