A square in a triangle
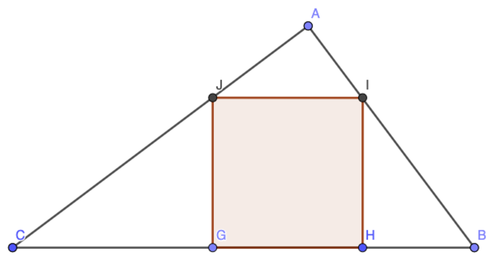
In the figure △ A B C is a right triangle with legs A B = 6 and A C = 8 . A square is drawn as shown, with a side along B C and corners on A B and A C . Find the length of the side of the square.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let ∠ A C B = α . Then tan α = 4 3 .
Let the length of each side of the square be a . Then
( 3 4 + 1 + 4 3 ) a = 6 2 + 8 2 = 1 0
⟹ a = 3 7 1 2 0 .
Nice Mr. Alak
I have a derived formula about problems like this. Let x be the side length of the square. Then,
x = b + h b h where: b is the side of the triangle where the side of the square coincides and h is the perpendicular distance from b to the opposite vertex.
Note that △ A B C is the popular pythagorean triple, 3 − 4 − 5 right triangle. So the length of B C is 1 0 . Now we need to find h ,
sin ∠ A B C = B C A C = A B h
1 0 8 = 6 h
h = 5 2 4
Now, substitute.
x = b + h b h = 1 0 + 5 2 4 1 0 × 5 2 4 = 3 7 1 2 0 a n s w e r
B C = 1 0 (pythagorean theorem) l e t H G = x = H I = G J △ A B C ∼ △ H B I ⇒ H B A B = H I A C ⇒ H B = 4 3 x △ A B C ∼ △ G C J ⇒ G C A B = G J A C ⇒ G C = 3 4 x B C = B H + H G + G C ⇒ 1 0 = 1 2 3 7 x ⇒ x = 3 7 1 2 0
We note the right △ A B C is the popular right triangle with integer side lengths of ratio 3 : 4 : 5 or 0 . 6 : 0 . 8 : 1 . We also note that △ A I J and △ B I H are similar to △ A B C .
Let the side length of the square be a , then A I = 0 . 6 a and I B = 0 . 8 a . Since:
A I + I B 0 . 6 a + 0 . 8 a 0 . 8 0 . 4 8 a + a ⟹ a = A B = 6 = 6 = 1 . 4 8 4 . 8 0 = 3 7 1 2 0