A square pyramid?

Geometry Level pending

You have a square with side length 2 and 4 identical triangles, each with two sides of length 3 \sqrt{3} and one side of length 2. When you glue them all together to form a square pyramid, what is its volume?

Give your answer to 3 decimal places.


The answer is 1.333.

Geoff Pilling by Geoff Pilling , 53, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Geoff Pilling
Feb 6, 2017

Since the height of this square pyramid will be 1 1 , six of these will fit together perfectly to make a 2 2 x 2 2 x 2 2 cube. Therefore the volume of the pyramid will be 8 6 ≈ 1.333 \frac{8}{6} \approx \boxed{1.333}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

That's a nice geometric argument. Alternatively, once you get the height, you can use the formula V = 1 3 A h V=\tfrac{1}{3}Ah , which works for any cone.

Brian Moehring - 4 years, 4 months ago

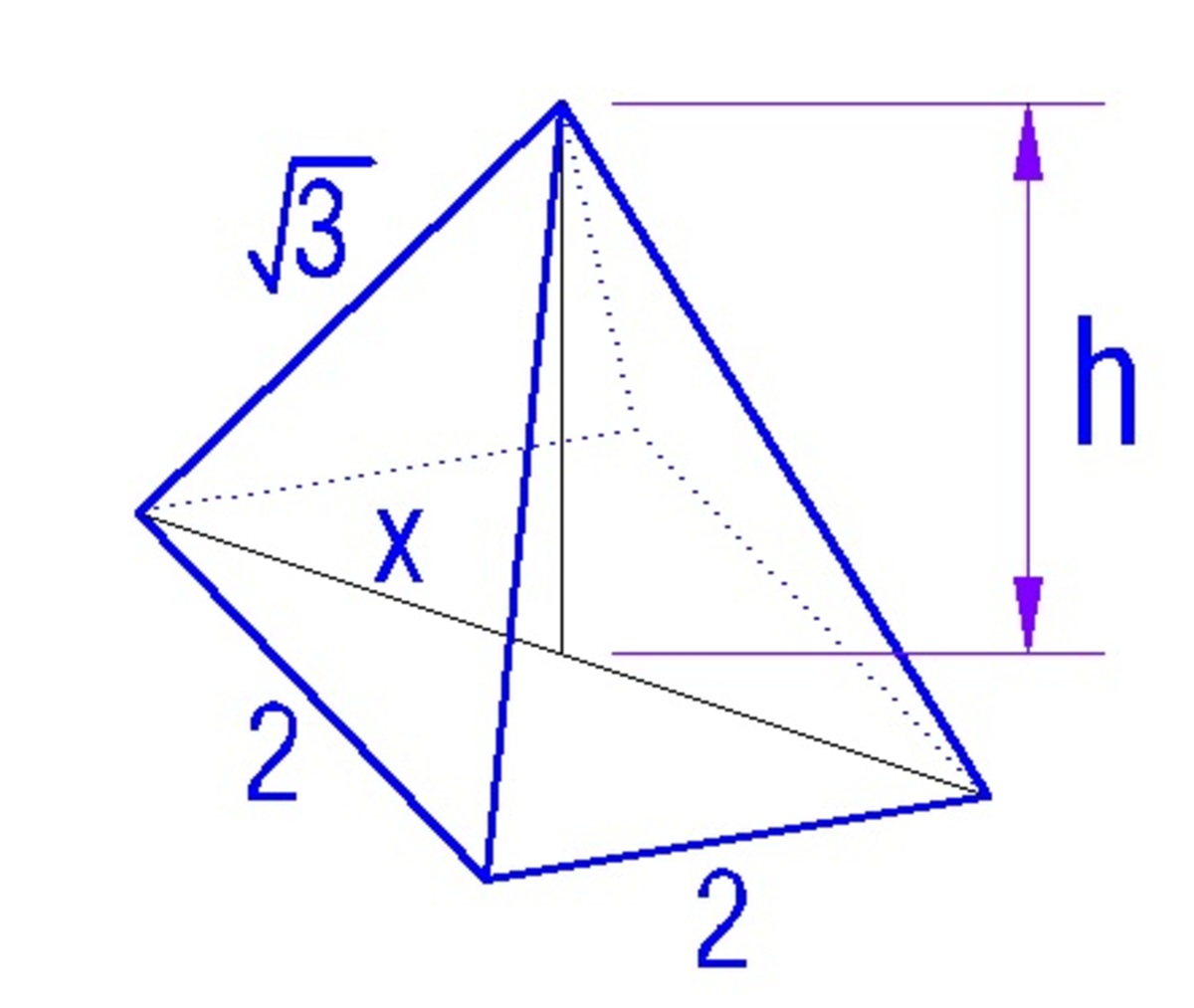x = x = half of the diagonal of the base = 2 2 + 2 2 2 = 2 = \frac{\sqrt{2^2+2^2}}{2} = \sqrt{2}

solving for the height., we obtain

h = ( 3 ) 2 − ( 2 ) 2 = 1 h = \sqrt{(\sqrt{3})^2 - (\sqrt{2})^2} = 1

The volume of a pyramid is given by the following formula.

V = 1 3 A b a s e ∗ h V = \frac{1}{3}A_{base} * h

V = 1 3 ∗ 4 ∗ 1 = 4 3 = 1.333 V = \frac{1}{3} * 4 * 1 = \frac{4}{3} = 1.333

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...