A squeezing spring

Classical Mechanics Level 3

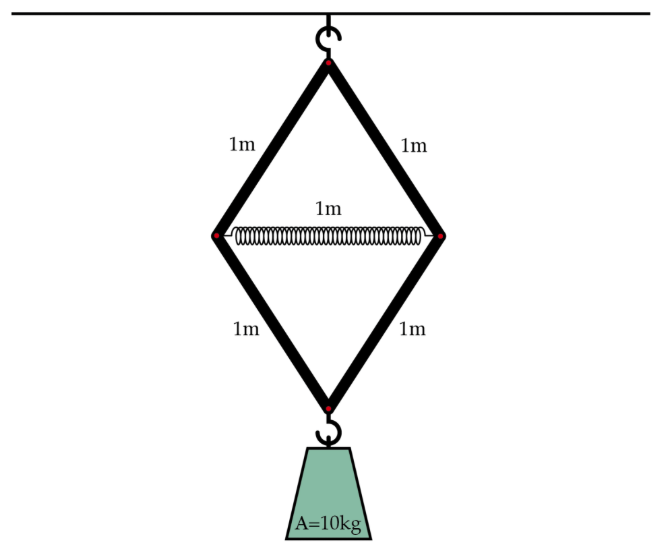A spring and four bars are hung from the ceiling in the configuration above. Each of the bars can pivot and rotate where it meets the other bar. The spring has a natural length of 1 m and a spring constant of 1000 N/m, while each of the bars has a length of 1 m and is effectively massless. A 10 kg weight is then hooked on to the bottom of this contraption at point A, causing the spring to squeeze. When the system comes to equilibrium, what is the length of the spring in meters ?

Details and assumptions

  • The acceleration of gravity is − 9.8 m / s 2 -9.8~m/s^2 .
  • The spring doesn't squeeze all that much, so you may assume that the vertical angles on the top and bottom remain at 60 + ϵ 60+\epsilon degrees, where ϵ \epsilon is a small angle.


The answer is 0.946.

David Mattingly by David Mattingly

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Mattingly Staff
May 13, 2014

The equilibrium point of the system after the weight is added will be at the minimum of potential energy. There is both gravitational and spring potential energy in the system. If t h e t a theta is the angle between the lower right bar and the vertical axis, then h h , the change in height of the mass, is

h = 2 ( c o s π / 6 − c o s θ ) h=2(cos~\pi/6-cos \theta) .

The compression distance d d of the spring, meanwhile, is

d = 1 − 2 s i n θ d=1-2sin \theta .

The total potential energy of the system is the sum of the spring potential and gravitational potential,

U = 1 2 k d 2 + m g h U=\frac {1} {2} k d^2 + m g h , which evaluates to

U = 500 ( 1 − 2 s i n θ ) 2 − 20 × 9.8 ( c o s θ − c o s π / 6 ) U=500 (1-2sin \theta)^2 - 20 \times 9.8 (cos \theta - cos~\pi/6) .

Minimizing this with respect to θ \theta gives the solution. We minimize by taking the derivative and setting it equal to zero, i.e.

0 = − 100 c o s θ ( 1 − 2 s i n θ ) + g s i n θ 0=-100 cos \theta (1-2 sin \theta)+gsin \theta .

If we define θ = π / 6 + ϵ \theta=\pi/6+\epsilon , where ϵ < < 1 \epsilon<<1 , we can use trigonometric identities and the small angle approximation to solve for ϵ = − 0.0309 \epsilon=-0.0309 . The length of the spring is L = 2 s i n ( π / 6 + ϵ ) = 0.946 L=2sin(\pi/6+\epsilon)=0.946 m.

3 Helpful 1 Interesting 1 Brilliant 2 Confused

this solution uses one approximation regaaurding the value of \epsilon
but the problem can be solved by an another method also............. let us take 2x to be the displacement of the block in downward direction..........

we can calculate the new length of the spring geometrically using pythagorus theorum.......in terms of x

let l be the new length of spring

further we form the energy equation..... mg*2x=(1/2)K(1-l)^2

solving ....i got an answer different from the given.....answer..and since i did not use any approximatio ...i think mine is more correct

Yash Sharma - 6 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...