A stereographic manipulation

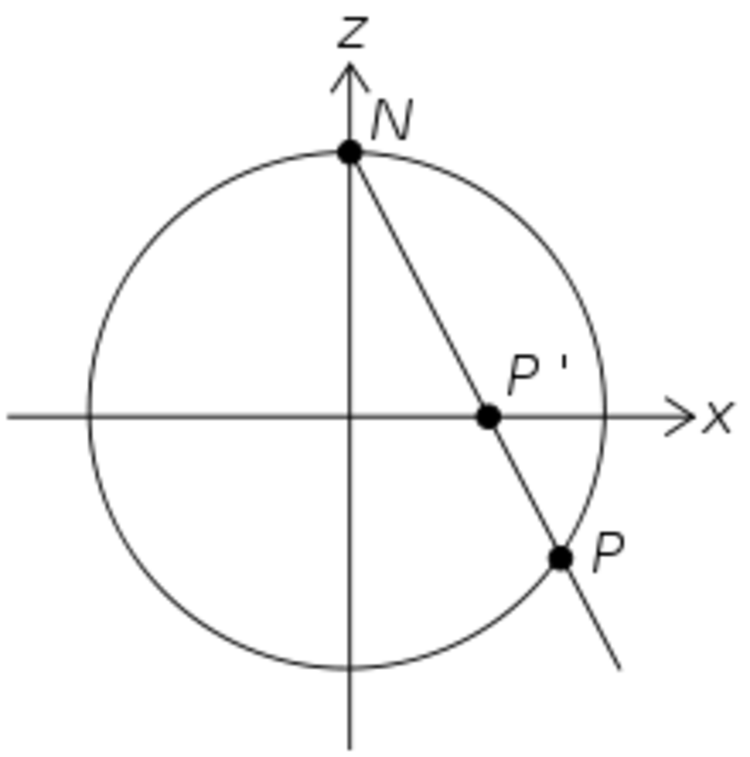
Let $S^1 = \{ (x,y) \in \mathbb{R} \backslash x^2+y^2 = 1 \}$ . Consider the stereographic projection :

Let $\mathcal{L}$ be the line passing through the point $N=(0,1) \in S^1$ and some point $P=(x,y) \in S^1$ such that $(x,y) \neq (0,1)$ . Then $\mathcal{L}$ crosses the x-axis at a point $P'=(\overline{x},0)$ . This defines a mapping : $f : S^1 \backslash \{ (0,1) \} \rightarrow \mathbb{R}$ $(x,y) \mapsto \overline{x}=f(x,y)$

Now, do the same, but this time, with the line $\mathcal{L'}$ passing through the point $(0,-1) \in S^1$ . Call the new function it induces by $f'$ .

What is $(f+f')(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} )$ ?

Credit : Google Image.