A Straight Line Doesn't Minimize the Action

Classical Mechanics Level 5

According to the Principle of Least Action , the path of a particle through space (given some caveats) is the path which minimizes the "action". Define the action $S$ as follows:

$\large{S = \int_{t_1}^{t_2} (E - U) \, dt}$

In the above formula, $E$ is the particle's kinetic energy and $U$ is the particle's potential energy. If a particle travels between two specific points in a definite amount of time $(t_2 - t_1 = T)$ , the path taken will be the one which minimizes the associated action $S$ .

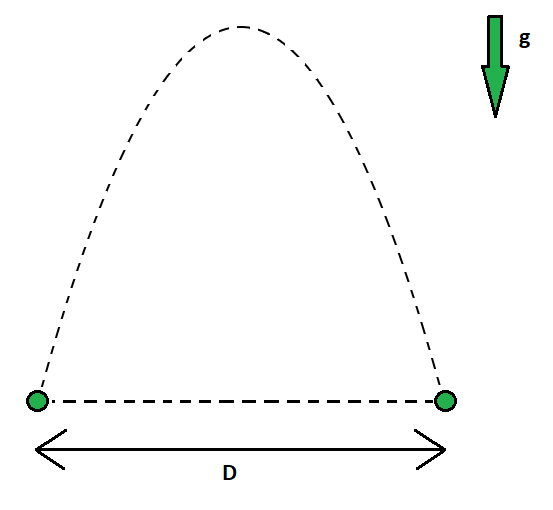
Let's consider an example. Suppose we have two points with the same vertical position, which are separated horizontally by a distance $D$ . Suppose also that there is a downward (vertical) gravitational acceleration $g$ , with an associated potential. Consider a particle of mass $m$ traveling between these two points in a definite time $T$ . Evaluate the actions for the following two paths:

1) A parabolic path consistent with standard kinematic principles (this is the path a real object would take)
2) A straight-line, constant-velocity path from one point to the other

Assume that $U = 0$ corresponds to the vertical position of the start and end points. The action for the straight-line path is greater than the action for the parabolic path by the following amount (hence, the parabolic path is favored):

$\large{\Delta S = \frac{m \, g^2 \, T^3}{\alpha}}$

Here, $\alpha$ is a positive integer. Determine the value of $\alpha$ .

The answer is 24.

1 solution

Steven Chase
Dec 25, 2017

Straight Path

Consider the straight-line, constant-velocity path. Let $(x,y) = (0,0)$ represent the start point on the left.

$x = \frac{D}{T} \, t \\ y = 0 \\ v_x = \frac{D}{T} \\ v_y = 0$

Kinetic energy and potential:

$E = \frac{1}{2} m \frac{D^2}{T^2} \\ U = 0$

Action:

$S = \int_0^T \frac{m \, D^2}{2 T^2} \, dt = \frac{m \, D^2}{2 T}$

Parabolic Path

The parabolic path is the one we are familiar with from kinematics. We know that $y = 0$ when $t = T$ :

$0 = v_{y0} \, T - \frac{1}{2} g \, T^2 \\ v_{y0} = \frac{g T}{2}$

Position and velocity expressions:

$x = \frac{D}{T} \, t \\ y = \frac{g T}{2} t - \frac{g}{2} \, t^2 \\ v_x = \frac{D}{T} \\ v_y = \frac{g T}{2} - g t$

Kinetic Energy:

$E = \frac{1}{2} m (v_x^2 + v_y^2) \\ = \frac{1}{2} m \Big [ \frac{D^2}{T^2} + (\frac{g T}{2} - g t)^2 \Big ] \\ \frac{1}{2} m \Big [ \frac{D^2}{T^2} + \frac{g^2 T^2}{4} -g^2 T t + g^2 t^2 \Big ]$

Potential Energy:

$U = m g \, y = m g \Big(\frac{g T}{2} t - \frac{g}{2} \, t^2 \Big)$

Action:

$S = \int_0^T (E - U) \, dt \\ = \int_0^T \Big[ \frac{1}{2} m \Big [ \frac{D^2}{T^2} + \frac{g^2 T^2}{4} -g^2 T t + g^2 t^2 \Big ] - m g \Big(\frac{g T}{2} t - \frac{g}{2} \, t^2 \Big) \Big] \, dt \\ = \frac{1}{2} m \Big [ \frac{D^2}{T} + \frac{g^2 T^3}{4} - \frac{g^2 T^3}{2} + \frac{g^2 T^3}{3} \Big ] - m g \Big(\frac{g T^3}{4} - \frac{g T^3}{6} \Big) \\ = \frac{m \, D^2}{2 T} + m g^2 T^3 \Big(\frac{1}{8} - \frac{1}{4} + \frac{1}{6} - \frac{1}{4} + \frac{1}{6} \Big) \\ = \frac{m \, D^2}{2 T} - \frac{m g^2 T^3}{24}$

We see therefore that the $\large{\frac{m D^2}{2T}}$ term is common to both actions, and that the parabolic action is smaller by:

$\Delta S = \frac{m g^2 T^3}{24}$

A Straight Line Doesn't Minimize the Action

The answer is 24.

1 solution

0 pending reports