A Strange Board Game

Logic Level 5

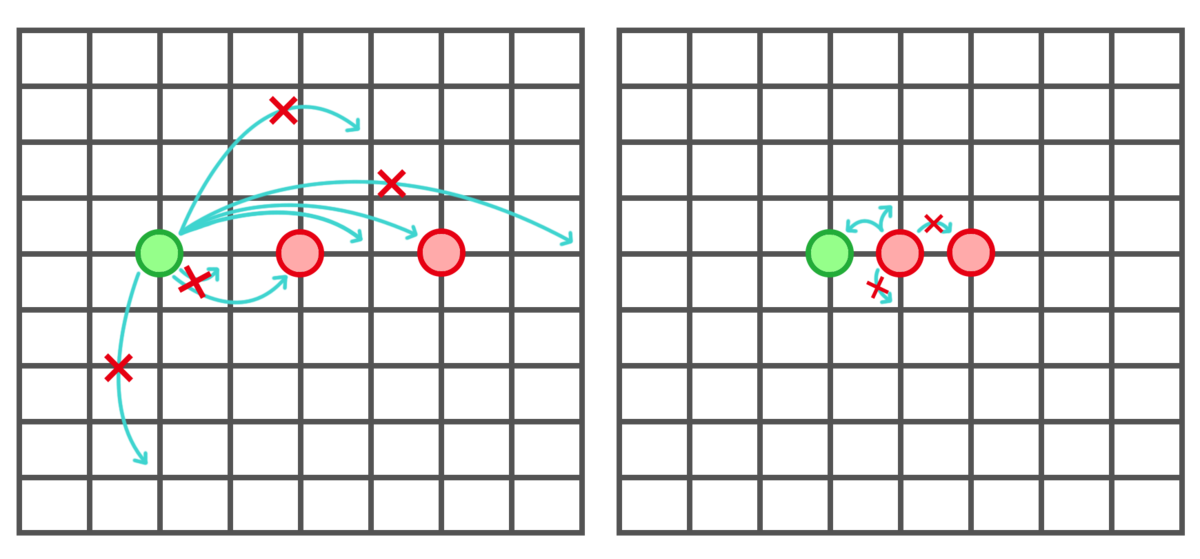
There is a board game. The rules are like below:

Green side and Red side take turns to move. In each turn, one side can only move one of her pieces to another crossing of the grid.
Green side can move her green piece over exactly one red piece along a straight line that is drawn on the board, while that red piece stays intact. (The piece "jumps over" a red piece.) The piece can capture a red piece if that piece lies on the destination. The piece can neither jump over another green piece nor capture it.
Red side can move her red piece to an adjacent crossing along the line, except downwards . It can capture a green piece if that piece lies on the destination. It cannot move to the wanted destination if another red piece lies on the destination.
If the Green side can't or doesn't want to move, it's okay for her to pass . (a.k.a. doesn't move any of her pieces) However, the Red side must make a move .

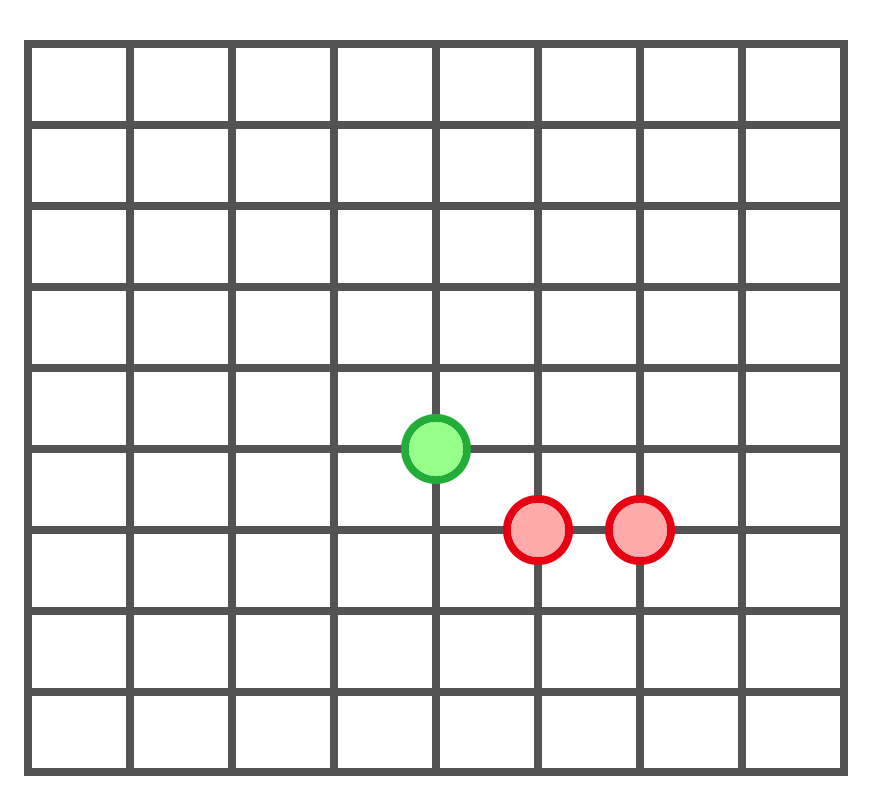
Consider there's a battle between green and red like above. If the Red side starts first, how many moves does Red side have to make in order to catch the Green side's piece, given that the Green side tries her best to delay the capture ?

The pieces are limited to the shown board, and the edge of the board is also a valid position to occupy.

4 5 6 It is not possible. 8 7 3 9

1 solution

Boi (보이)
Aug 12, 2017

Name each column as $1,~2,~3,~\cdots,~9$ from the left and name each row as $A,~B,~C,~\cdots,~J$ from above.

Then the correct moves are as follows:

${\color{#D61F06}{G7\rightarrow G8}}$

${\color{#20A900}{\text{(cannot move)}}}$

${\color{#D61F06}{G8\rightarrow G9}}$

${\color{#20A900}{\text{(cannot move)}}}$

${\color{#D61F06}{G6\rightarrow F6}}$

${\color{#20A900}{F5\rightarrow F8}}$

${\color{#D61F06}{F6\rightarrow E6}}~\leftarrow~\text{Personally, I think this is the hardest part.}$

${\color{#20A900}{\text{(cannot move)}}}$

${\color{#D61F06}{G9\rightarrow F9}}$

${\color{#20A900}{\text{(cannot move)}}}$

${\color{#D61F06}{F9\rightarrow F8}}$

The answer is $\boxed{6}.$

This board game's Green side uses the "Cannon" and Red side uses the "Soldier" from the Korean chess named Janggi , which comes from the Chinese chess named Xiangqi.

I think that it should be stated that the pieces are limited to the board shown. I had assumed the board was infinite and thus capture would be impossible.

Daniel Branscombe - 3 years, 10 months ago

Added the condition! Thanks :D

Boi (보이) - 3 years, 10 months ago

I thought in step F5->F8 the red piece F6 should be eaten? I don't think u state it in the question.

Zhi Yang Marcus - 3 years, 9 months ago

I already stated: "Green side can move her green piece over exactly one red piece orthogonally, while that red piece stays intact ."

Boi (보이) - 3 years, 9 months ago

How about ${\color{#D61F06}G6->F6}$ , ${\color{#20A900}F5->F9}$ , ${\color{#D61F06}G7->F7}$ , ${\color{#D61F06}F7->F8}$ , ${\color{#D61F06}F8->F9}$ ?

Atomsky Jahid - 3 years, 9 months ago

If red moves from F7 to F8, then the green can capture the red piece on F6.

Boi (보이) - 3 years, 9 months ago

Understood the fault in my moves.

Atomsky Jahid - 3 years, 9 months ago

Isn't it important to mention that the edge of the board is a valid position to occupy too?.I had assumed that G9 and F9 weren't valid crossings

gy abhishek - 3 years, 6 months ago

Thank you, I've updated the problem!

Boi (보이) - 3 years, 6 months ago

A Strange Board Game

1 solution

0 pending reports