A strange equation II
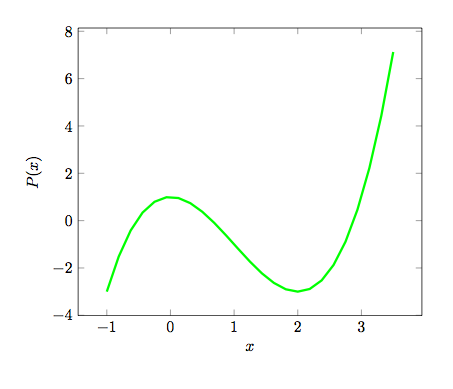 The three real roots of the polynomial
P
(
x
)
=
x
3
−
3
x
2
+
1
can be expressed as:
The three real roots of the polynomial
P
(
x
)
=
x
3
−
3
x
2
+
1
can be expressed as:
x 1 = − b cos ( e ° ) + a , x 2 = − c cos ( f ° ) + a , x 3 = d cos ( g ° ) + a ,
where x 1 < x 2 < x 3 , 0 ° < e < 9 0 ° , 0 ° < f < 9 0 ° , 0 ° < g < 9 0 ° , such that a , b , c , d , e , f and g are positive integers; and e , f and g are integer degrees. Find a + b + c + d + e + f + g .
You may also try Part III .
The answer is 147.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The quick way of solving y 3 − 3 y − 1 = 0 is to use the substitution y = 2 cos z , which gives us
8 cos z − 6 cos z − 1 = 0 ⇒ cos 3 z = 2 1
This gives us z = 2 0 , 1 0 0 , 1 4 0 , and choosing the correct signs to take 1 8 0 − z would give us the values of 2 0 , 4 0 , 8 0 that you calculated.
Note: A possible tricky part is explaining why 2 cos 2 0 ∘ + 1 has a unique expression in that form. I don't immediately see why this has to be true. Any thoughts?
Log in to reply
But we dont know that y is between -2 and 2. Please explain if I am wrong
Log in to reply
We can solve for ∣ cos θ ∣ > 1 by extending the definition of the trigonometric function into the complex plane. In this case, as it turns out, we do not need to do so.
Just saying, you've duplicated the proof of Cardan's method. In this case, that is, the irreducible case of the cubic, trigonometry helps to find the roots as pointed out by Calvin Lin. You might want to refer to some old books for many such examples and exercises.
Let's substitute x = y + 1 in order to delete the x 2 coefficient: ( y + 1 ) 3 − 3 ( y + 1 ) 2 + 1 = 0 y 3 − 3 y − 1 = 0
Now, there comes the tricky part. Let's assume the identity ( u + v ) 3 − 3 u v ( u + v ) − ( u 3 + v 3 ) = 0 and make it match with the equation: y = u + v − 3 u v = − 3 ⇔ u v = 1 − ( u 3 + v 3 ) = − 1 ⇔ u 3 + v 3 = 1
Now, another trick: cube both sides of the first equation: u v = 1 ⇔ ( u ) 3 ( v ) 3 = 1
With this, we have an equation system that matches with a second degree equation, so let's z 1 = u 3 and z 2 = v 3 : z 2 − z + 1 = 0
Use the quadratic formula: z 1 , 2 = 2 1 ± i 3
And substitute back for u and v : u = 3 2 1 + i 3 v = 3 2 1 − i 3 Where i = − 1 is the imaginary unit.
Express them in the polar form: u = 3 e i ( 3 π + 2 π k ) ⇔ u = e 9 π i ( 6 k + 1 ) v = 3 e − i ( 3 π + 2 π k ) ⇔ v = e − 9 π i ( 6 k + 1 ) Where k = 0 , 1 , 2
Reverse to the rectangular form and convert from radians to degrees: u = cos ( 2 0 ° ( 6 k + 1 ) ) + i sin ( 2 0 ° ( 6 k + 1 ) ) v = cos ( 2 0 ° ( 6 k + 1 ) ) − i sin ( 2 0 ° ( 6 k + 1 ) )
Now, for k = 0 : u = cos ( 2 0 ° ) + i sin ( 2 0 ° ) v = cos ( 2 0 ° ) − i sin ( 2 0 ° ) So, y = u + v : y = cos ( 2 0 ° ) + i sin ( 2 0 ° ) + cos ( 2 0 ° ) − i sin ( 2 0 ° ) y = 2 cos ( 2 0 ° ) And, x = y + 1 : x = 2 cos ( 2 0 ° ) + 1
Now, for k = 1 : u = cos ( 1 4 0 ° ) + i sin ( 1 4 0 ° ) ↔ u = − cos ( 4 0 ° ) + i sin ( 4 0 ° ) v = cos ( 1 4 0 ° ) − i sin ( 1 4 0 ° ) ↔ v = − cos ( 4 0 ° ) − i sin ( 4 0 ° ) So, y = u + v : y = − cos ( 4 0 ° ) + i sin ( 4 0 ° ) − cos ( 4 0 ° ) − i sin ( 4 0 ° ) y = − 2 cos ( 4 0 ° ) And, x = y + 1 : x = − 2 cos ( 4 0 ° ) + 1
And finally, for k = 2 : u = cos ( 2 6 0 ° ) + i sin ( 2 6 0 ° ) ↔ u = − cos ( 8 0 ° ) − i sin ( 8 0 ° ) v = cos ( 2 6 0 ° ) − i sin ( 2 6 0 ° ) ↔ v = − cos ( 8 0 ° ) + i sin ( 8 0 ° ) So, y = u + v : y = − cos ( 8 0 ° ) − i sin ( 8 0 ° ) − cos ( 8 0 ° ) + i sin ( 8 0 ° ) y = − 2 cos ( 8 0 ° ) And, x = y + 1 : x = − 2 cos ( 8 0 ° ) + 1
We obtained three solutions for x , and after ordering them, we have: x 1 = − 2 cos ( 4 0 ° ) + 1 x 2 = − 2 cos ( 8 0 ° ) + 1 x 3 = 2 cos ( 2 0 ° ) + 1
So, a = 1 , b = c = d = 2 , e = 4 0 , f = 8 0 and g = 2 0 , and a + b + c + d + e + f + g = 1 4 7