A Strange Point in a Triangle
Geometry
Level
3
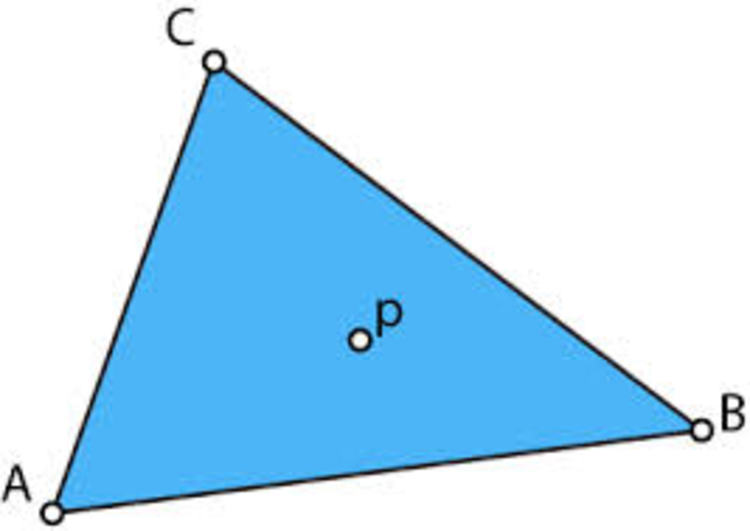Given a triangle ABC and a point P inside the triangle such that |PA| = 4 cm, |PB| = 5 cm and |PC| = 6 cm , If the perimeter of the triangle is maximum then the point P is the __ of triangle ABC .
Incentre
Centroid
Circumcentre
Data insufficient
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
First of all an easy observation to be proved.
Observation
Solution
Now coming back to the Question, P is a moving point in a triangle such that its distances from the vertices is constant (Given in the question).
Let angle AOB is (\theta) and P is a moving point in the interior of angle AOB such that OP is Constant, PM and PN are normals from the point P to OA and OB. TO PROVE - OM + ON is Maximum when P lies on angular bisector of angle AOB.
So for Perimeter to be maximum P must lie on angular bisector of angle A, B and C
Hence P is the Incentre