A strange similarity
Recall that two quadrilaterals are similar if they can be obtained from scaling each other.
Bobby has a quadrilateral and wants to construct a similar quadrilateral using the following method. For each a side of the quadrilateral, he draws a line parallel to that side but units away.
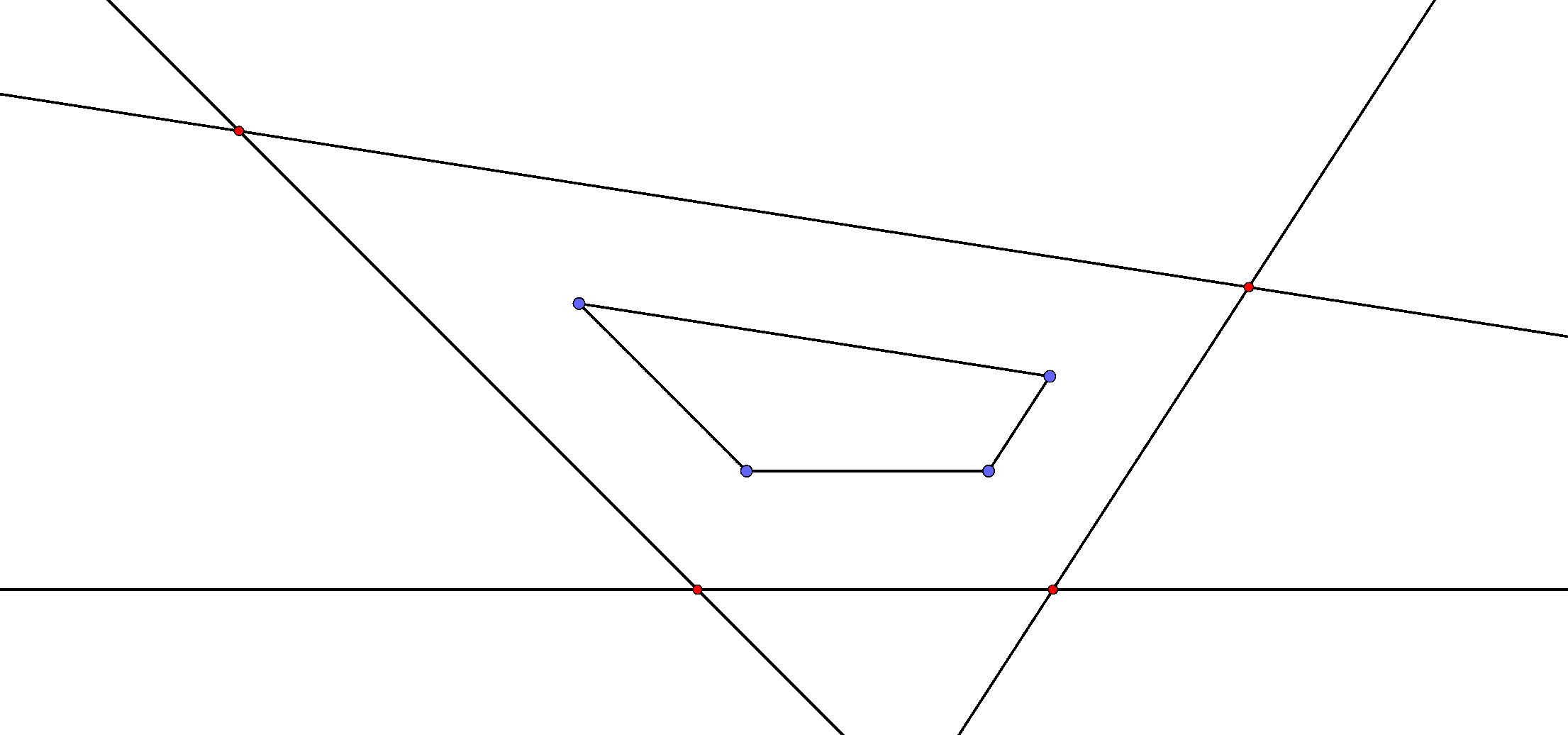
The line intersect at new points (red in the picture) and form a new quadrilateral. Because the angles are the same, Bobby thinks the new quadrilateral is similar to the original one. Alas, quadrilateral are not as nice as triangles... For which of the following families of quadrilaterals will actually Bobby get a similar quadrilateral:
1: squares
2: rhombi which are not squares
3: rectangles which are not squares
4: convex kites which are not rhombi
5: concave kites
6: parallelograms which are neither rectangles nor rhombi
Give your answer as follows: (where ) is 1 if you think quadrilaterals in the said category will give rise to similar quadrilaterals with this construction, and 0 otherwise. Then write your answer as the number . For example, if you believe 2, 4 and 6 are positive, then write 010101 (= 10101) as your answer.
The answer is 110110.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The answer is squares, rhombi and (concave and convex) kites. More precisely, the answer is positive for any tangential quadrilateral. Indeed, up to similarity, one can always assume a tangential quadrilateral has an incircle of radius one, and this circle touches the quadrilateral at a point which is at 0°. So, up to similarity, what defines a tangential quadrilateral is the location (say in degrees) of the other 3 points on the circle where the tangents touch. Upon preforming the transformation, the point of contact remain at the same angles (but on a circle of radius 1 + x ). Hence 1 + x is the factor in the similarity.
It is also a characterisation of such quadrilaterals: see there .