A Strange Star in a Strange Shape
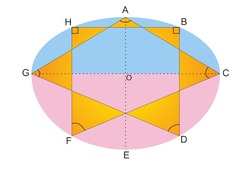 A strange shape can be made by joining two semi-ellipses with same major axis, but different minor axes. The above image is an example of one such shape. The blue region is a semi-ellipse with semi-minor axis
(
O
A
)
of length
3
. The pink region is a semi-ellipse with semi-minor axis
(
O
E
)
of length
4
. The major axis
(
G
C
)
, common to both semi-ellipses has a length of
1
0
.
A strange shape can be made by joining two semi-ellipses with same major axis, but different minor axes. The above image is an example of one such shape. The blue region is a semi-ellipse with semi-minor axis
(
O
A
)
of length
3
. The pink region is a semi-ellipse with semi-minor axis
(
O
E
)
of length
4
. The major axis
(
G
C
)
, common to both semi-ellipses has a length of
1
0
.
Now, a 7 - pointed star in inscribed in this strange shape, symmetric about line A E , such that B H is parallel to major axis, ∠ H = 9 0 ∘ , and line G C bisects angles ∠ C and ∠ G .
Calculate ∠ A + ∠ B + ∠ C + ∠ D + ∠ F + ∠ G + ∠ H .
Give your answer in degrees.
This problem is a part of the set - A Strange Shape
The answer is 540.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Actually it can be resolved simpler: The 3 angles of triangle AGC is equal to 180. Then angle F + angle MCF + angle B is equal to total angles of triangle FMC. Similar to triangle GKD. Therefore total of 7 angle is 180 + 180 +180 = 540
its simple, triangle AOG,AOC,FMC,DKG,ARE ALL RIGHT ANGLE TRIANGLE,and sum of all angles are simply 90+90+90+90+90+90=540
We have 7 yellow triangles, the base angles of those 7 yellow triangles form the exterior angles of heptagon.The sum of exterior angles are 2 (360) = 720 So <A + <B + < C+<D +< F+<G +< H = 7(180) – 720 = 540
Nice approach, this is much simpler than what I did.
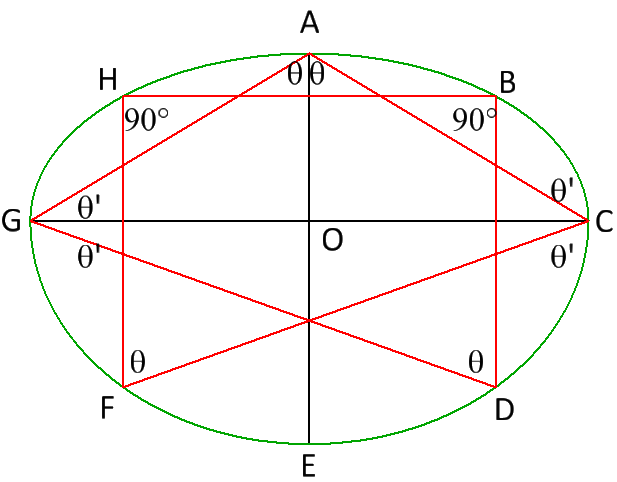 Start traversing the star from A in the counter-clockwise direction -
Start traversing the star from A in the counter-clockwise direction -
Let ∠ O A G = θ .
Then ∠ A G O = θ ′ it's compliment.
Since GC bisects ∠ A G D , ∠ O G D = θ ′ as well.
∠ G D B = θ compliment of compliment
∠ D B H = 9 0 ° and ∠ B H F = 9 0 ° are given.
Had we started traversing from A in the clockwise direction, we would have got -
∠ O A C = θ
∠ A C O = θ ′
∠ O C F = θ ′
∠ C F H = θ
Adding them all we have θ + θ ′ + θ ′ + θ + 9 0 ° + 9 0 ° + θ + θ ′ + θ ′ + θ = 4 θ + 4 θ ′ + 1 8 0 ° = 5 4 0 °
i just got it without solving... haha ... crap that was just a big mistake
In triangle AGC, A+(G/2)+(C/2)=180. Now, F+(C/2)=90 & D+(G/2)=90. Hence, A+B+C+D+E+F+G+H=540.
A 7 - pointed star is called a heptagram (or a septagram). There are two types of heptagrams possible { 7 / 2 } and { 7 / 3 } . For more info, click here
The above drawn heptagram is a { 7 / 2 } heptagram.
For any { 7 / 2 } heptagram , the sum of the angles of its vertices is constant. I shall now prove it to be 5 4 0 ∘ .
I have labeled the heptagram as following. Notice that I J K L M N P is a heptagon. Heptagon
Heptagon
Let the required sum ∠ A + ∠ B + ∠ C + ∠ D + ∠ F + ∠ G + ∠ H be x .
We can make seven quadrilaterals by choosing 3 non-adjacent vertices, of the heptagram and one corresponding side of the heptagon.
One such quadrilateral, A N F C is highlighted in the diagram. As the sum of interior angles of quadrilateral is 3 6 0 ∘ , We get the following equations for each quadrilateral.
∠ A + ∠ G + ∠ C + ∠ G L C = 3 6 0 ∘
∠ A + ∠ C + ∠ F + ∠ A N F = 3 6 0 ∘
∠ A + ∠ D + ∠ G + ∠ A J D = 3 6 0 ∘
∠ B + ∠ H + ∠ F + ∠ F K B = 3 6 0 ∘
∠ B + ∠ G + ∠ D + ∠ B P G = 3 6 0 ∘
∠ B + ∠ H + ∠ D + ∠ L M N = 3 6 0 ∘
∠ C + ∠ H + ∠ F + ∠ J I P = 3 6 0 ∘
By adding these equations, we get
3 x + ∠ G L C + ∠ A N F + ∠ A J D + ∠ F K B + ∠ B P G + ∠ L M N + ∠ J I P = 2 5 2 0 ∘
Notice ∠ G L C + ∠ A N F + ∠ A J D + ∠ F K B + ∠ B P G + ∠ L M N + ∠ J I P is sum of interior angles of heptagon, ie 9 0 0 ∘ .
Solving for x , we get,
3 x + 9 0 0 ∘ = 2 5 2 0 ∘
3 x = 1 6 2 0 ∘
x = 5 4 0 ∘