A surprising answer
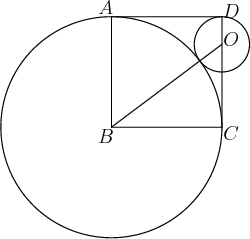 In the diagram, the circle centered at
B
and the circle centered at
O
are tangent inside square
A
B
C
D
. If
cos
∠
O
B
C
=
b
a
for coprime positive integers
a
and
b
, then what is
a
+
b
?
In the diagram, the circle centered at
B
and the circle centered at
O
are tangent inside square
A
B
C
D
. If
cos
∠
O
B
C
=
b
a
for coprime positive integers
a
and
b
, then what is
a
+
b
?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
i just guessed....
I just did it in my head
Just an extra step for those who are wondering how to get from 3 to 4:
1 + R r = 4 1 + 1
⟹ r R + r = 4 1 + 4
the cos is only intimidating lol
exactly what i did
I did the same way
a and b are prime? what does it mean?
Log in to reply
"a and b are relatively prime" means they dont have a common factor. thus, a/b is in simplest form. remember, 4/5 is also equal to 8/10 giving the problem another issue :)
Good one !
My solution was identical. I even denoted the radii with the same letters : )
Log in to reply
Me too! Same to same equations and variable.
Nice Solution
I too used the same method. Is it so difficult !!
This is WAAAAY too easy for a 400-point question. I mean, it's just simple pythagorean theorem and equating...
Solved it the same way! I can't believe this is a level 5 problem...
Log in to reply
I looked at it and thought level 2 and was very surprised.
Same way...no pens are needed ;)
I also do thissssss Coool bro
how to solve it by trigonometry
it is given that a and b are prime, hence a cannot be 4
Log in to reply
No, it says that a and b are relatively prime, which implies that the largest integer that divides a and b is 1. The fact that two integers are relatively prime does not imply that they must both be prime.
I liked Adiya's way, but my way is informal, lets take the radius of big circle be 1 and that of small circle be R . In right triangle OBC, O B = 1 + R , O C = 1 − R Using Pythagoras, R = 4 1 Now cos ∠ O B C = 1 + 1 / 4 1 = 5 4 Ans 4 + 5 = 9
Cool..I could think of neither this nor that :(.
Next time, use \cos code in LaTeX which makes appear c o s as cos .
Also, give the sign of angle before O B C , which is obtained by code \angle that is, ∠ .
As a moderator I can edit this in your solution, but I want YOU to do that... @Sanjeet Raria
I used the same method. Is. It so difficult !!
This is simple yet completely logical. Thank you so much!
Why have they given the relatively prime part of the question?
Log in to reply
because 4/5 = 8/10 = 12/15 which will give the problem another issue without the "relatively prime" part :)
Hey, it' s "Using The Pythagorean Theoram" and not "Using Pythagoras". LOL!
Hi! Remember that you only need 4 lines of DO to equal 1 line BC
Just the pythagorean! BC = 4, OC = 3 , and BO = 5! now just put the requirements 4+5 = 9 :P
I may be loosing something, but where is said that the radius of the smaller circle is equal to 1? If it is not, the only thing I think we can state is that a + b = 9 times the radius of this smaller circle...
Let the large and small circle be respectively:
C i r c l e ( B , R ) ; C i r c l e ( O , r ) ;
Let θ = ∠ O B C , and let T be the tangent point between circles; we have:
∣ B O ∣ = ∣ B T ∣ + ∣ T O ∣ = R + r ;
∣ B C ∣ = R ;
∣ C O ∣ = ∣ C D ∣ − ∣ O D ∣ = R − r ;
by Pytagoras’ theorem:
∣ B C ∣ 2 + ∣ C O ∣ 2 = ∣ B O ∣ 2 ;
R 2 + ( R − r ) 2 = ( R + r ) 2 ;
simplyfing:
R ( R − 4 r ) = 0 ; R = 4 r ;
c o s θ = ∣ B O ∣ ∣ B C ∣ = R + r R = 4 r + r 4 r = 5 r 4 r = 5 4 = b a ;
a + b = 4 + 5 = 9 ;
θ = a r c c o s ( 5 4 ) = 3 6 . 8 6 9 8 9 7 6 5 d e g
Let radius of circle with center B be R and circle with center O be r .
In △ O B C ,
O B 2 = O C 2 + B C 2 ......... Pythagoras' theorem
∴ Property of touching circles ( R + r ) 2 = OC=CD-OD=R-r ( R − r ) 2 + R 2 ∴ R 2 + 2 R r + r 2 = R 2 − 2 R r + r 2 + R 2 ∴ R 2 = 4 R r ∴ R r = 4 1 ⟹ R R + r = 4 1 + 4 Adding 1 on both sides ∴ B C O B = 4 5 ∴ cos ∠ O B C = 5 4
Hence answer is 4 + 5 = 9