A tale of (not so) many cities
The Queen plans to build a number of new cities in the wilderness, connected by a network of roads. She expects the annual tax revenues from each city to be numerically equal to the square of the population. Road maintenance will be expensive, though. The annual cost for each road is expected to be numerically equal to the product of the populations of the two cities that road connects. To keep the costs for road maintenance down, the Queen decrees that there should be only one way to get from any city to any other, and not more than three roads should connect to any given city (the attached design would be acceptable, for example).
Unfortunately, Parliament is responsible for deciding which roads will be built (subject to the two Queen's decrees) and how many people live in each city, but has no concern for attempting to stay financially solvent (meaning tax revenue ≥ road maintenance). Regardless of what Parliament decides, what is the largest number of cities that the Queen can build without risking to lose money?
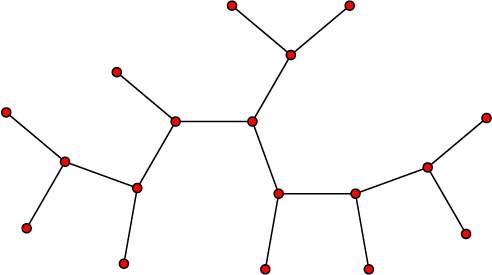
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Interesting solution! Is there anything special about this structure?
If you arrange an infinite number of cities around the perimeter of a circle, each with one road coming in and one going out the tax revenue of population squared equals the cost of two roads (2x1/2(your population x your neighbors population)). So you can have an infinite number of cities providing they stick to 2 roads each. Or, if they average <=2 roads each.
Log in to reply
The circle violates the no-more-than-one-route rule, but your idea is good. The problem is that efficiency is not a consideration. The statement, "regardless of the ... design of the roads" implies that the roads will be built as inefficiently as possible.
The given quadratic form (revenue - cost) is positive definite for finite Dynkin graphs and positive semidefinite for extended Dynkin graphs, as for the graph D 5 ~ shown in the picture on top. D 5 ~ is the smallest extended Dynkin graph if we don't allow points of order 4. If you add one vertex and one edge to such an extended Dynkin graph, you make it indefinite. See here
"Regardless of the design of the roads" in the problem means that, within the constraints, we should be always allowed to choose the least economical solution? (Sorry, this wasn't so clear to me from the formulation...)
How is it even possible to solve this without knowing the funding in the first place ?
I got this wrong because I included the trivial solution where the 7th city has population zero
Inadequately specified question, paticularly bearing in mind that the 'valid' example shown has 18 cities.
The question is either very oddly formulated or something is wrong. I could put a first city with a population of 3 n inhabitants. Attach to this first city 3 cities with 1 inhabitant.
The revenue is now 3 2 n − 3 n + 1 which is still positive. So I have enough money to add a lot of cities. Say I add only cities with 1 inhabitant, then every extra edge costs 1 (because each edges joins two cities with population 1 each). So I can at least 3 2 n − 3 n + 1 cities (I'm just ignoring the revenue of the 1-inhabitant cities at this point). Since there is no bound on n , there is no bound on the number of cities...
Note that if the huge city is connected to less small cities then the cost go down even more. The number of edges remain the same since we are in a tree (it's the number of cities minus 1).
So it seems the original intended problems on quadratic forms got lost in the translation to the Queen's story...
Log in to reply
You are forgetting the role of Parliament in this: The Queen does not get to pick the populations. Revenue may exceed cost for the populations you choose, but not for others.
Could you prove that there is no losing configuration without cities of order 3? Try as I might, I cannot come up with a proof myself.
Log in to reply
If you have a string of cities with populations a , b , c , . . . , then the revenue-cost function will be half of a 2 + ( a − b ) 2 + ( b − c ) 2 + . . . , which will be positive.
Suppose two cities populations are P and P − p . The cost of a road between them is P ( P − p ) while the contribution of the second city is only ( P − p ) ( P − p ) . Every time you add a city, therefore, you change net revenue by − p ( P − p ) . This is greatest in magnitude (just as any product with a fixed sum is) when the factors are equal. That is, when p = 2 P .
In the worst case scenario, whenever the Queen increases the number of cities by 1, the Parliament will connect it to the most populated existing city available and populate the new city with half of that city's population. This tree is made of descending chains. If the only cities with less than three roads have population 1, you will have to scale the chain it belongs to by 2 and scale all chains descending off it by 2 too, just to make a new city fit while keeping revenue minimised. Scaling a chain by 2 is still always good for revenue so we must aim to keep chains short and prefer to add a new chain rather than scale an existing one.
So what arrangement and length of chains will satisfy this problem? A single city doesn't break the bank. The next case to check should be 3 cities adjacent to a 4th central city as this has as many chains as possible of length 2 without extra scaling. This arrangement has positive revenue so there's no need to check smaller cases. The next largest trees with chain length 2 look similar to Otto's answer of 6 cities, which has revenue 0, so no need to check smaller (or equal) cases. Scaling the graph will just scale 0 to 0 and so adding any cities to this will make the revenue negative. Hence, we have the answer.
if 4 cities are built, and "smart guys" at the parliament build 3 roads per city, that is 4n^2 tax money and 6n^2 repair costs... so with only 4 cities she risks loosing money, no?
Log in to reply
The graph is supposed to be a tree; there is supposed to be only one way to get from any city to any other.
If you make each of the 6 cities have a population of 1, it fails to meet the criteria:
The total taxes generated are 6 (being the sum of the squares of each city).
The total road maintenance cost is 10 (being the sum of the populations at each end of each segment).
Have I misunderstood the question? I don't see a single solution above 2 cities that meets the criteria, with populations of 1 in each city.
Log in to reply
The cost for road maintenance will be 5 in this case, leaving a little profit for the Queen.
We will look at various cases, depending on how many cities there are with three neighbors (vertices "of order three" in graph theory).
The most interesting case is that of two such cites. The simplest case involves 6 cities, as shown in the attached figure. Completing squares, we can write the revenue-cost function as 2 1 ( c − d ) 2 + 4 1 ( 2 a − c ) 2 + 4 1 ( 2 b − c ) 2 + 4 1 ( 2 e − d ) 2 + 4 1 ( 2 f − d ) 2
There is no losing configuration here, but there are break-even configurations, when c = d = 2 a = 2 b = 2 e = 2 f . For example, we can make c = d = 4 and a = b = e = f = 2 . Now we can easily construct a losing configuration with 7 cities by adding one more city, with a population of 1, and connecting it to one of the cities with population a , b , e or f . Revenue will go up by 1, but cost will go up by 2.
If there is no city of order 3, then there are no losing configurations. If there is only one city of order 3, then the smallest losing configuration involves 8 cities. This case was carefully analyzed here . (The smallest graph with a losing configuration corresponds to m = n = 2 and p = 3 in that post.)
Thus they can build at most 6 cities without risking to lose money.