A tangent ellipse and a bounded area
An ellipse with a semi-major axis of units and a semi-minor axis of units, is positioned and oriented such that it is tangent to two rays. The first ray is the positive half of the -axis, while the second ray is half of the line , with . This is shown in the figure below. The tangency point with the -axis is given as . Determine this ellipse, then find the area bounded by the two rays and the ellipse (shaded in light blue). If this area is , then enter .
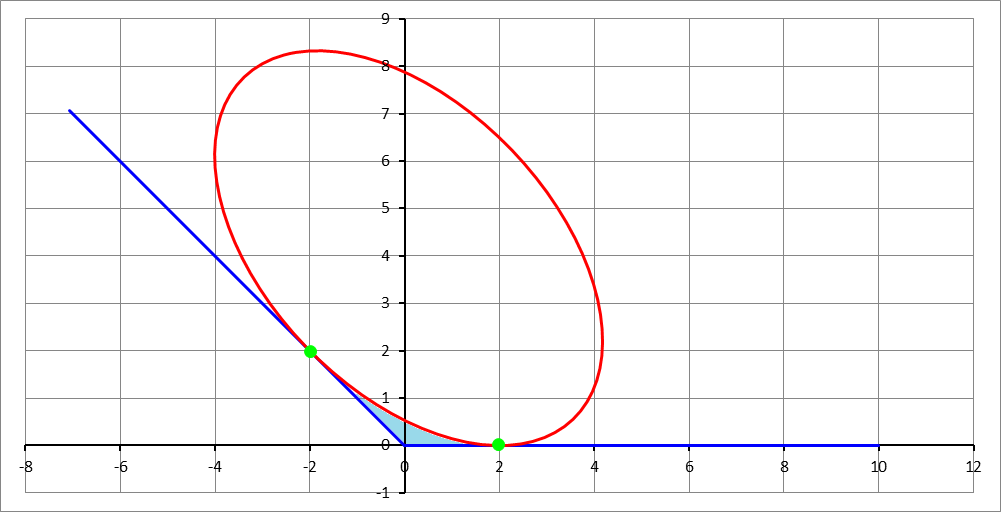
Note: To determine the ellipse you may need to use the iterative multivariate Newton-Raphson root finding method.
The answer is 725.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Very well known equation of ellipse with semi-major and semi-minor axis equal to 5 and 3, respectively, is: 2 5 x 2 + 9 y 2 = 1 This is the equation of ellipse in coordinate system where x and y axis coincide with semi-major and semi-minor axis, respectively, and where center of ellipse coincide with origin of coordinate system. However, when we rotate coordinate axis for some angle θ and translate the origin to some point ( p , q ) , the equation of ellipse changes according to these transformations and becomes:
( x − p ) 2 ( 2 5 cos 2 θ + 9 sin 2 θ ) + ( y − q ) 2 ( 9 cos 2 θ + 2 5 sin 2 θ ) + 2 2 5 1 6 ( x − p ) ( y − q ) sin 2 θ = 1
Differentiating above equation we get equation involving the slope at some point ( x , y ) on ellipse:
d x d [ ( x − p ) 2 ( 2 5 cos 2 θ + 9 sin 2 θ ) + ( y − q ) 2 ( 9 cos 2 θ + 2 5 sin 2 θ ) − 2 2 5 1 6 ( x − p ) ( y − q ) sin 2 θ ] 2 ( x − p ) ( 2 5 cos 2 θ + 9 sin 2 θ ) + 2 ( y − q ) d x d y ( 9 cos 2 θ + 2 5 sin 2 θ ) − 2 2 5 1 6 ( y − q + ( x − p ) d x d y ) sin 2 θ = d x d 1 = 0
We know coordinates of one point - ( 2 , 0 ) - and we know that the slope is 0 at that point. On the other hand, we know that the other point lies on line y = − x which is tangent to ellipse, which provide us with information that the point is of the form ( x , − x ) and that slope is -1 at that point. Thus, we constitute four equations in for unknowns ( p , q , θ , x ):
( 2 − p ) 2 ( 2 5 cos 2 θ + 9 sin 2 θ ) + q 2 ( 9 cos 2 θ + 2 5 sin 2 θ ) − 2 2 5 1 6 ( 2 − p ) q sin 2 θ 2 ( 2 − p ) ( 2 5 cos 2 θ + 9 sin 2 θ ) + 2 2 5 1 6 q sin 2 θ ( x − p ) 2 ( 2 5 cos 2 θ + 9 sin 2 θ ) + ( x + q ) 2 ( 9 cos 2 θ + 2 5 sin 2 θ ) + 2 2 5 1 6 ( x − p ) ( x + q ) sin 2 θ 2 ( x − p ) ( 2 5 cos 2 θ + 9 sin 2 θ ) + 2 ( x + q ) ( 9 cos 2 θ + 2 5 sin 2 θ ) − 2 2 5 1 6 ( p − q − 2 x ) sin 2 θ = 1 = 0 = 1 = 0
I've used Matlab's fsolve function with initial guess ( p , q , θ , x ) = ( 0 , 4 . 5 , − π / 4 , − 2 ) to solve this non-linear system. Solutions I got were: ( p , q , θ , x ) = ( 0 . 0 8 0 2 7 3 , 4 . 1 6 3 5 9 2 , − 0 . 8 0 6 3 7 3 , − 2 . 0 1 3 1 7 5 ) .
Area is then found to be A = 0 . 7 2 4 9 6 5 6 6 7 5 1 2 3 0 1 and ⌊ 1 0 0 0 A ⌋ = 7 2 4 . Proposed correct answer is actually 725 and this slight difference is, I assume, due to accuracy of numerical methods employed.