A Tangential Trapezoid
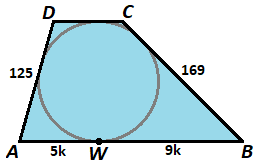
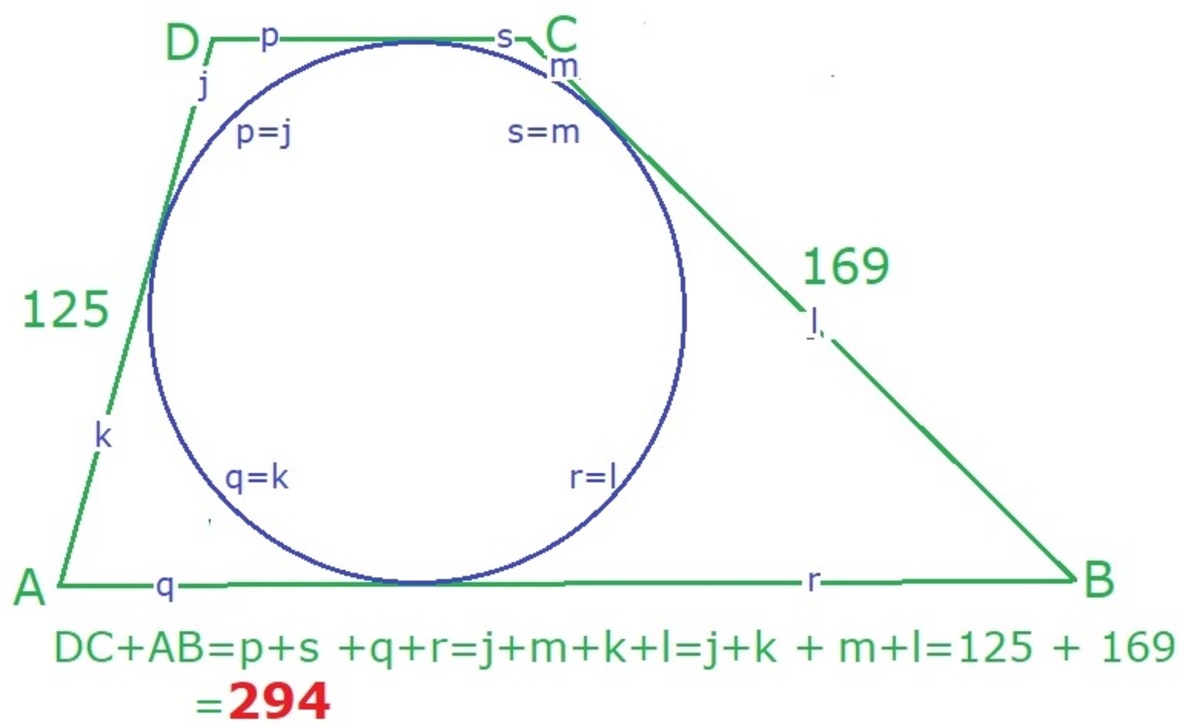
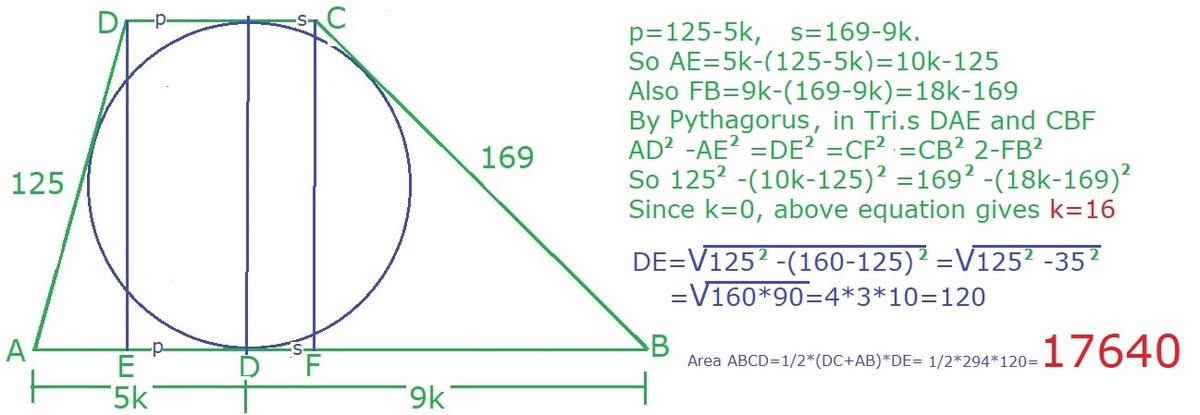
A tangential trapezoid A B C D has legs A D = 1 2 5 and B C = 1 6 9 and its longest base A B is divided by the tangent point W of its incircle at a ratio of B W A W = 9 5 .
Find the area trapezoid A B C D .
The answer is 17640.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution!
This is all thanks to the information in the link from the problem.
Say the point of tangency between the circle and the side D C , then A W ⋅ D Y = B W ⋅ C Y , so we can write D Y = 9 l and C Y = 5 l for some l .
Since the pairs of tangent lengths from each vertex are equal (again, see the link for definitions), we have
5 k + 9 l = 1 2 5
and
9 k + 5 l = 1 6 9
Solving these, we find k = 1 6 and l = 5 , so the tangent lengths are ( e , f , g , h ) = ( 8 0 , 1 4 4 , 2 5 , 4 5 ) . The area of a tangential quadrilateral is given by
( e + f + g + h ) ( f g h + e f h + e g h + e f g ) = 1 7 6 4 0
This is a great solution, and much cleaner than how I solved it! Thanks for posting.
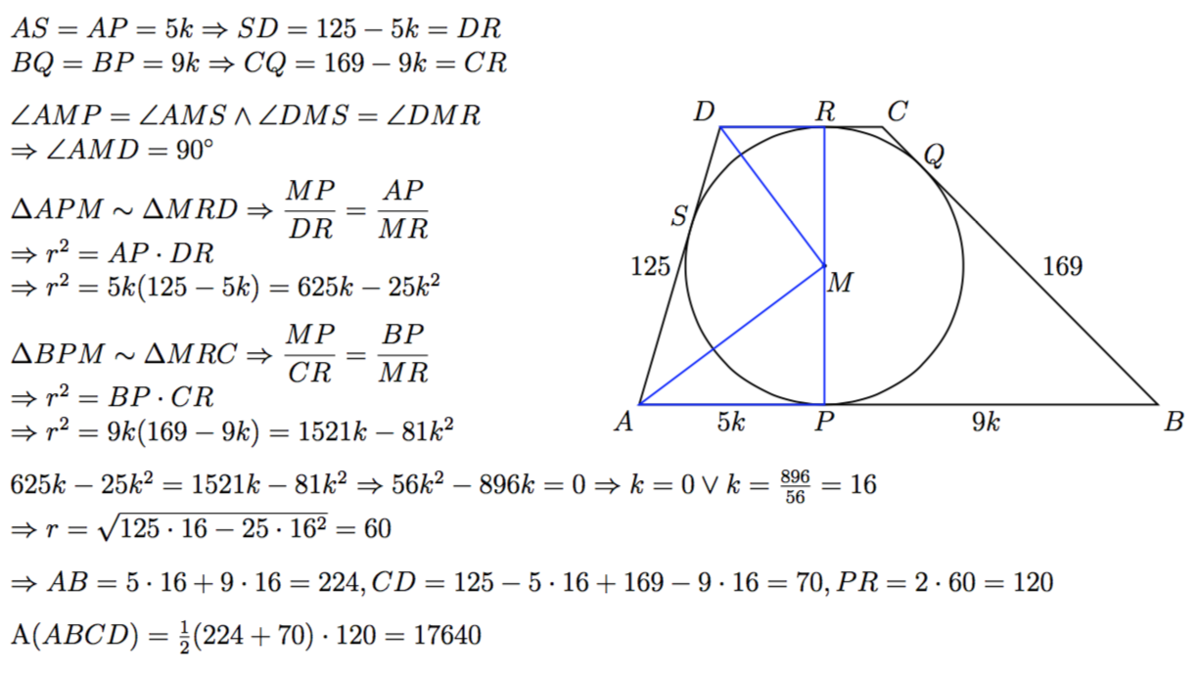
Let the tangent point on B C be X , the tangent point on C D be Y , and the tangent point on A D be Z . Let e = A W , f = B W , g = C Y , and h = D Y . Since tangent segments to a circle from the same external point are congruent, A Z = A W = e , B X = B W = f , C X = C Y = g , and D Z = D Y = h . Also drop perpendiculars from D to A B at U and from C to A B at V . Let the radius of the incircle be r , so the height of the trapezoid is W Y = C V = D U = 2 r .
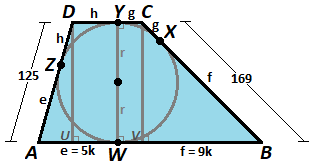
Using Pythagorean's Theorem on △ B C V , ( 2 r ) 2 + ( f − g ) 2 = ( f + g ) 2 , which simplifies to f g = r 2 . Likewise, using Pythagorean's Theorem on △ A D U , ( 2 r ) 2 + ( e − h ) 2 = ( e + h ) 2 , which simplifies to e h = r 2 .
Since the legs are A D = 1 2 5 and B C = 1 6 9 , e + h = 1 2 5 and f + g = 1 6 9 . Since B W A W = 9 5 , f e = 9 5 .
The five equations with five variables ( f g = r 2 , e h = r 2 , e + h = 1 2 5 , f + g = 1 6 9 , and f e = 9 5 ) solve to e = 8 0 , f = 1 4 4 , g = 2 5 , h = 4 5 , and r = 6 0 .
Therefore, the bases of the trapezoid are b 1 = e + f = 8 0 + 1 4 4 = 2 2 4 , b 2 = g + h = 2 5 + 4 5 = 7 0 , the height is h = 2 r = 2 ⋅ 6 0 = 1 2 0 , and the area of the trapezoid is A = 2 1 ( b 1 + b 2 ) h = 2 1 ( 2 2 4 + 7 0 ) 1 2 0 = 1 7 6 4 0 .