A tank obliquely cut
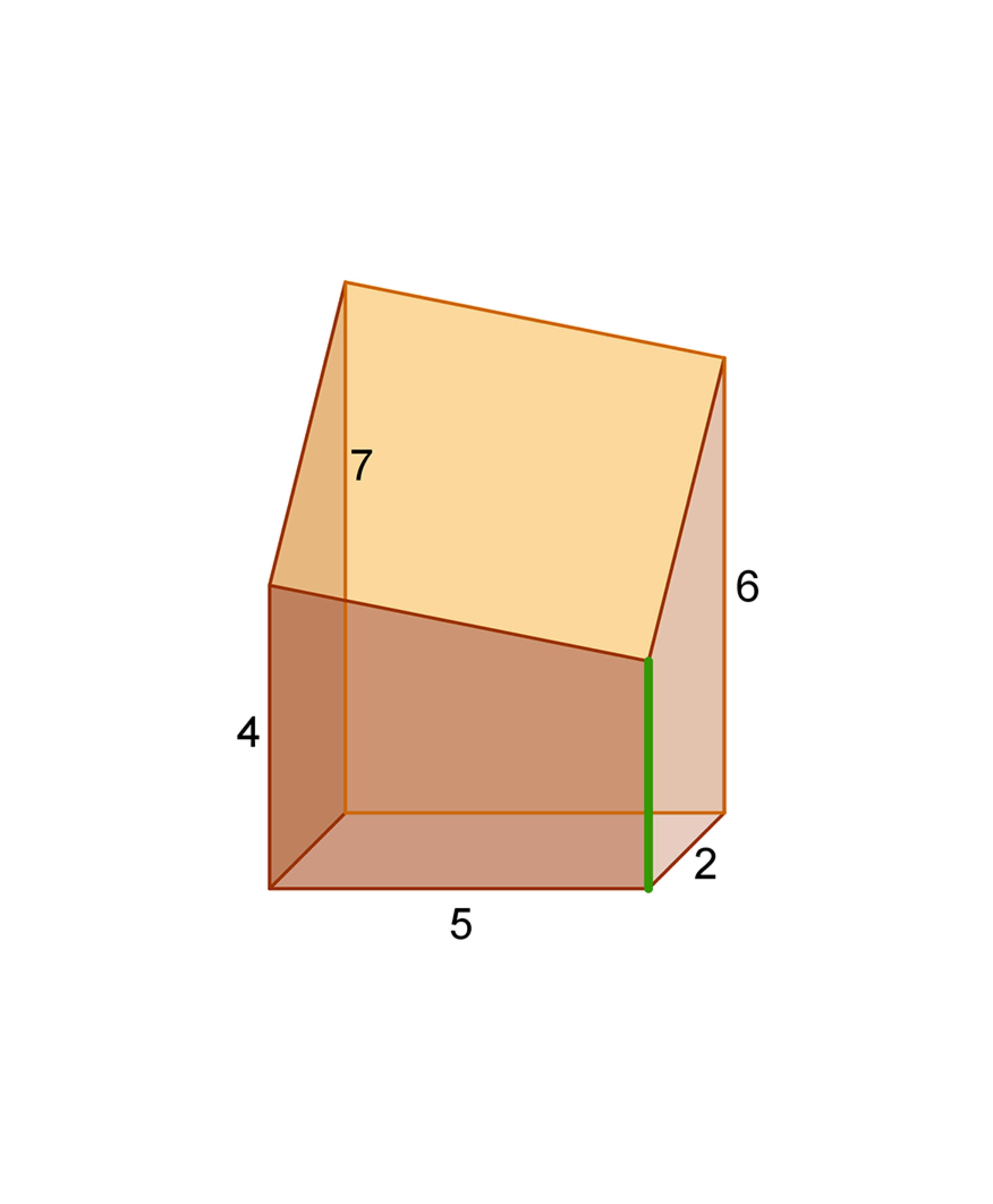
The top part of a tank that originally had a cuboid shape has been cut by a plane not parallel to its horizontal base, as seen in the picture. What is the volume of liquid the tank can hold, if we don’t tilt or move it in any way? The lengths of some edges are given in the picture (don’t bother with the measurement unit):
- dimensions of rectangular base: length 5 , width 2
- lengths of vertical edges (only three of them are known): 4 , 6 and 7
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
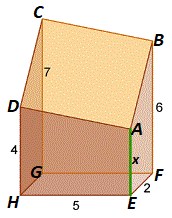
Since the length of the midsegment of a trapezium is half the sum of the lengths of the two parallel sides we get: ∣ ∣ M N ∣ ∣ = 2 ∣ ∣ D H ∣ ∣ + ∣ ∣ B F ∣ ∣ ⇒ ∣ ∣ M N ∣ ∣ = 2 4 + 6 ⇒ ∣ ∣ M N ∣ ∣ = 5 ∣ ∣ M N ∣ ∣ = 2 ∣ ∣ A E ∣ ∣ + ∣ ∣ C G ∣ ∣ ⇒ 5 = 2 ∣ ∣ A E ∣ ∣ + 7 ⇒ ∣ ∣ A E ∣ ∣ = 3 The tank can hold liquid up to the level of point A, hence the maximum volume is 2 × 5 × 3 = 3 0 . Clarification : obviously, the term “ trapezium ” is used here in the way Proclus and Archimedes defined it, i.e. the quadrilateral with a pair of parallel sides.