A TCS problem
Imagine a circle and a triangle put into a square. The square's side is the same as the circle's diameter. If the shaded area has
an area of π
, what is the area of the whole shape?
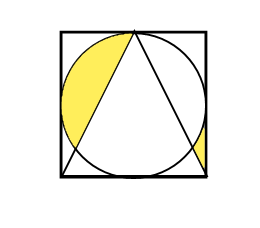
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the diagram below, let the circle have radius r :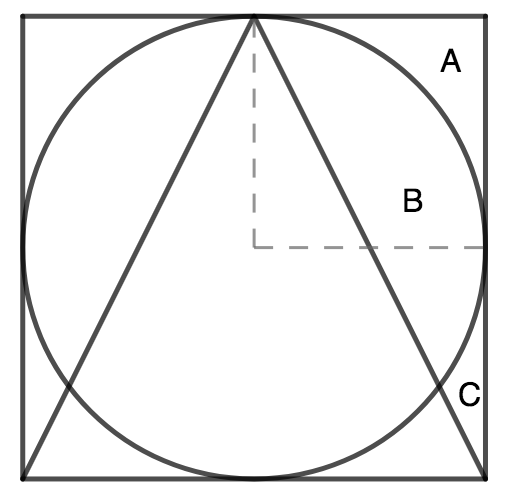
Consider the triangle formed by regions A, B and C. It has area r 2 . Note that [ B ] + [ C ] is the desired yellow area (where [ ⋅ ] represents the area of the region). [ A ] = r 2 − 4 π r 2 since it is a quarter of the square minus a quarter of the circle. Thus [ B ] + [ C ] = ( [ A ] + [ B ] + [ C ] ) − [ A ] = r 2 − ( r 2 − 4 π r 2 ) = 4 π r 2 . Since we are told that [ B ] + [ C ] = π , r 2 = 4 and r = 2 . Thus the area of the square is ( 2 r ) ( 2 r ) = 1 6