A titled ellipse inscribed in a triangle
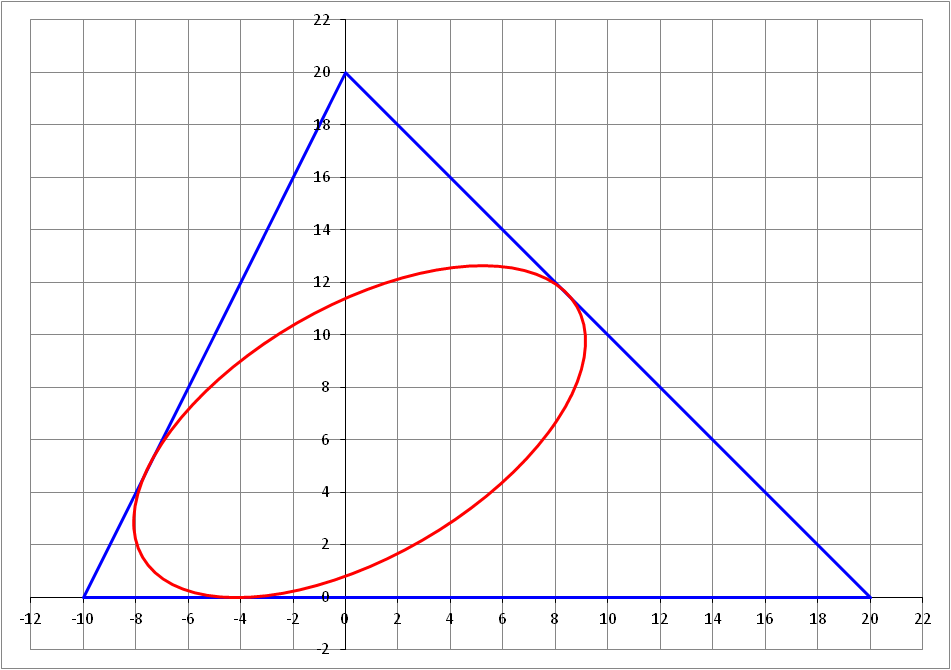
A triangle has its vertices at A ( 0 , 2 0 ) , B ( − 1 0 , 0 ) and C ( 2 0 , 0 ) , as shown in the figure above. We wish to fit an ellipse in the triangle with two conditions:
- The ratio of major axis to minor axis is 2.
- The angle that the major axis makes with the horizontal is 3 0 ∘ .
Find the length of the major axis of this ellipse. Round your answer to the nearest hundredth.
The answer is 19.09.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
No, i think your solution is probably the easiest. It is straight forward and to the point.

The general equation of an ellipse centered at r C and tilted by an angle θ counter clockwise from the positive x-axis is given by
( r − r C ) T R D R T ( r − r C ) = 1
where r = [ x y ] is any point on the ellipse
r C = [ x C y C ] is the center of the ellipse
R = [ cos θ sin θ − sin θ cos θ ]
D = ⎣ ⎢ ⎡ a 2 1 0 0 b 2 1 ⎦ ⎥ ⎤
From the conditions of the problem, the ellipse is tangent to the three sides of the triangle at unknown points
r 1 , r 2 and r 3 as shown in the figure.
The gradient of the ellipse is given by 2 R D R T ( r − r C ) . At the points of tangency its direction is known. The direction along the normal to the side of tangency. Therefore, we can write
R D R T ( r i − r C ) = α i n i for i = 1 , 2 , 3
where α i is some constant, and n i = [ cos ϕ i , sin ϕ i ] T where ϕ i is the angle that the normal to the side makes with the positive x-axis. We have ϕ 1 = 4 π , ϕ 2 = π − tan − 1 ( 2 1 ) , and ϕ 3 = − 2 π
From this, it follows that
r i = r C + α i R D − 1 R T n i = r C + α i R D − 1 R T [ cos ϕ i , sin ϕ i ] T
Since r i lies on the ellipse, it satisfies its equation, therefore,
α i 2 [ cos ϕ i , sin ϕ i ] R D − 1 R T [ cos ϕ i , sin ϕ i ] T = 1
At the point, we note the effect of the rotation matrix R T , on the normal vector [ cos ϕ i , sin ϕ i ] T .
It is evident that
R T [ cos ϕ i , sin ϕ i ] T = [ cos ( ϕ i − θ ) , sin ( ϕ i − θ ) ] T
Substituting this, we obtain an expression for α i , namely,
α i = a 2 cos 2 ( ϕ i − θ ) + b 2 sin 2 ( ϕ i − θ ) 1
Next, we note that the points r 1 lies on the line (the right side) whose equation is
[ cos ϕ 1 , sin ϕ 1 ] T ( r 1 − A ) = 0
Hence,
[ cos ϕ 1 , sin ϕ 1 ] T ( r 1 − r C + r C − A ) = 0
Substituting the expression for r 1 − r C from above, we get
α 1 [ cos ϕ i , sin ϕ i ] R D − 1 R T [ cos ϕ i , sin ϕ i ] T + [ cos ϕ 1 , sin ϕ 1 ] T ( r C − A ) = 0
This simplifies to,
α 1 1 + [ cos ϕ 1 , sin ϕ 1 ] T ( r C − A ) = 0
Substituting the expression for α 1 we obtain,
a 2 cos 2 ( ϕ 1 − θ ) + b 2 sin 2 ( ϕ 1 − θ ) + [ cos ϕ 1 , sin ϕ 1 ] r C = [ cos ϕ 1 , sin ϕ 1 ] A
At this point, we use the fact the a = 2 b , to get
a cos 2 ( ϕ 1 − θ ) + 4 1 sin 2 ( ϕ 1 − θ ) + [ cos ϕ 1 , sin ϕ 1 ] r C = [ cos ϕ 1 , sin ϕ 1 ] A
Similar equations can be obtained for r 2 and r 3 , they are listed below:
a cos 2 ( ϕ 2 − θ ) + 4 1 sin 2 ( ϕ 2 − θ ) + [ cos ϕ 2 , sin ϕ 2 ] r C = [ cos ϕ 2 , sin ϕ 2 ] A
a cos 2 ( ϕ 3 − θ ) + 4 1 sin 2 ( ϕ 3 − θ ) + [ cos ϕ 3 , sin ϕ 3 ] r C = [ cos ϕ 3 , sin ϕ 3 ] B
Hence, we ended up with three equations in the three unknowns: a , and the two coordinates of r C .
Now, let
E 1 = cos 2 ( ϕ 1 − θ ) + 4 1 sin 2 ( ϕ 1 − θ )
E 2 = cos 2 ( ϕ 2 − θ ) + 4 1 sin 2 ( ϕ 2 − θ )
E 3 = cos 2 ( ϕ 3 − θ ) + 4 1 sin 2 ( ϕ 3 − θ )
then, we have the following linear system of equations:
⎣ ⎡ E 1 E 2 E 3 cos ϕ 1 cos ϕ 2 cos ϕ 3 sin ϕ 1 sin ϕ 2 sin ϕ 3 ⎦ ⎤ ⎣ ⎡ a x C y C ⎦ ⎤ = ⎣ ⎡ 2 0 sin ϕ 1 2 0 sin ϕ 2 0 ⎦ ⎤
Solving the linear system, we obtain a = 9 . 5 4 5 , therefore, Major axis = 2 a = 1 9 . 0 9 .
My solution was enormously cumbersome. In summary:
I performed two transformations on the coordinates:
I then used Pythagoras' Theorem to find the lengths of the three sides of the triangle and used the formula for the inradius of a triangle, r = s ( s − a ) ( s − b ) ( s − c ) where a , b , c are the side lengths and s is half the perimeter of the triangle.
Finally I doubled this to get the diameter of the circle and doubled it again to reverse the effect of the second transformation and obtain the major axis of the ellipse, 19.09.
Now, tell me there must be a much easier approach?!