A touching problem...

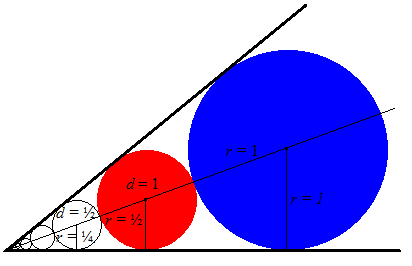
The bisector of the two lines passes through the centers of the 2 circles. So,

$Sin(\frac{1}{2}\theta)=\dfrac{1}{3}$ , or

$\theta = 2ArcSin(\dfrac{1}{3}) \approx 39$ degrees

(The two centers are separated by a distance of $1+2=3$ , while the difference in height is $2-1=1$ )

As with most geometry problems, this question is much easier to answer if you a add an extra line (and in this case, more circles). We can also use the similarity of these figures to our advantage. Continuing the relation, an infinite set of circles (whose diameters are decreasing by a ratio of ½) can be similarly added to the figure, each tangent to the next at only one point. Drawing a line from the vertex of the angle through the centers of these circles, we see that the hypotenuse of the triangle that is created is the radius of the largest circle (r = 1) and the sum of the diameters of all the smaller circles, or 1 + (1 + ½ + ¼ + ⅛ + ...) = 1 + 2 = 3.

So, the sine of the angle of the "thinner" vertex is ⅓. Thus, the angle of the "thicker" vertex is equal to 2sin(⅓) ≈ 39 degrees.