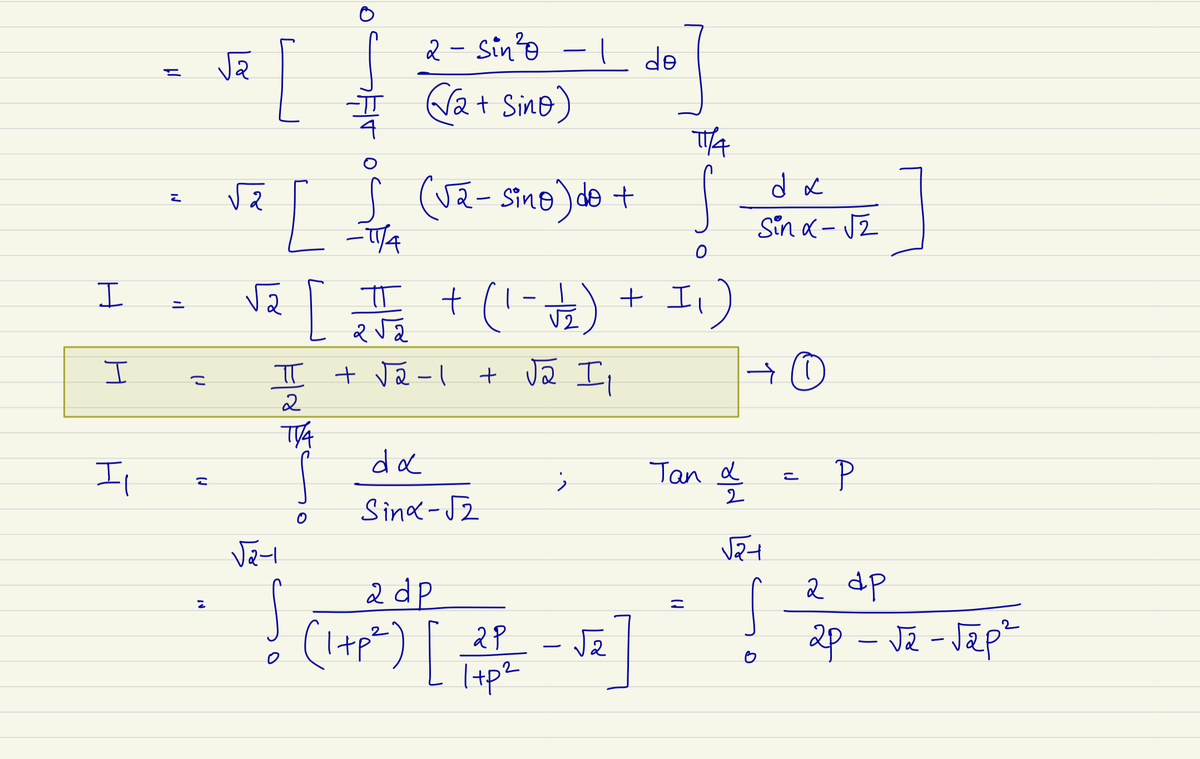
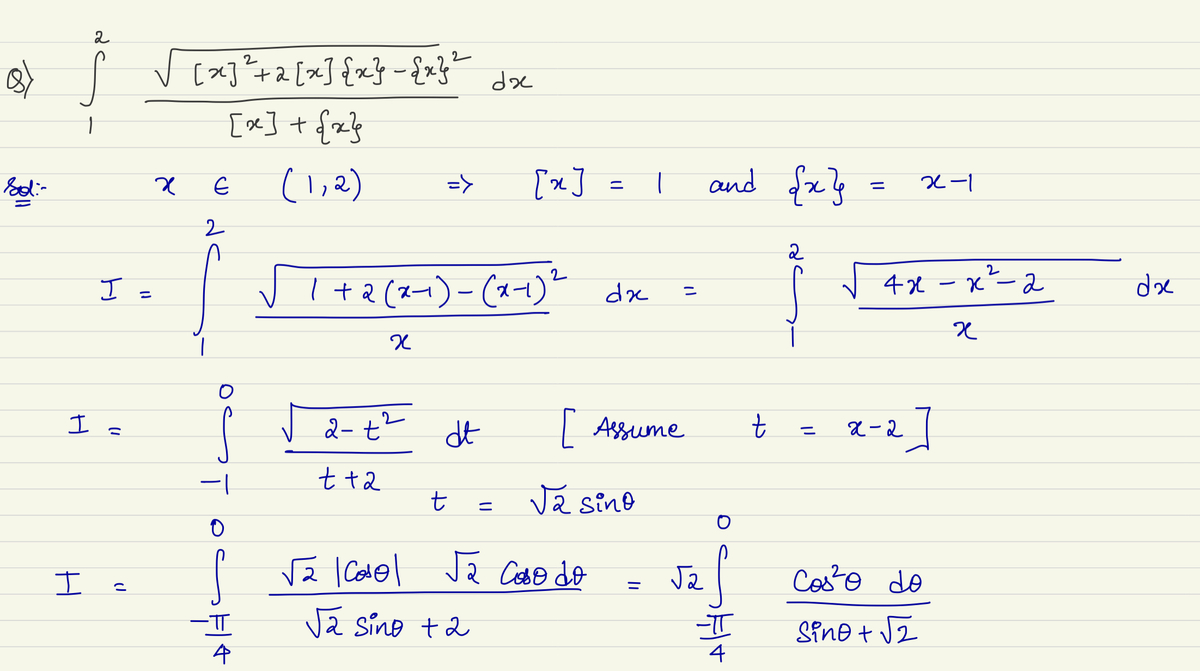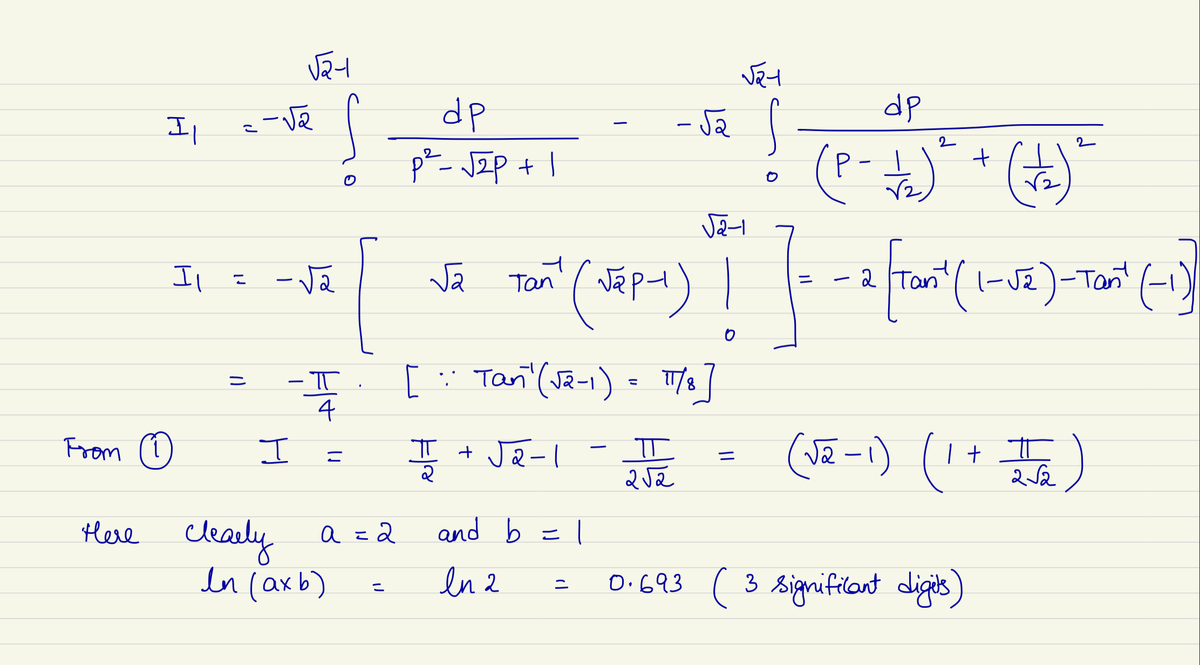A tough integral in disguise!

$\large \int_{1}^{2} \dfrac{ \sqrt { \lfloor x \rfloor ^{2} + 2 \lfloor x \rfloor \lbrace x \rbrace - \lbrace x \rbrace^{2} } }{ \lfloor x \rfloor + \lbrace x \rbrace } dx$

If the integral above equals to $(\sqrt{a} - b ) \left( b + \dfrac{ \pi}{ a\sqrt {a} } \right)$ , where $a$ and $b$ are coprime positive integers, find $\ln(a \times b)$ .

Notations :

• $\lfloor \cdot \rfloor$ denotes floor function .
• $\lbrace \cdot \rbrace$ denotes fractional part function .
• $\ln(\cdot)$ denotes logarithm to the base $e$ .