A Triangle. A Circle
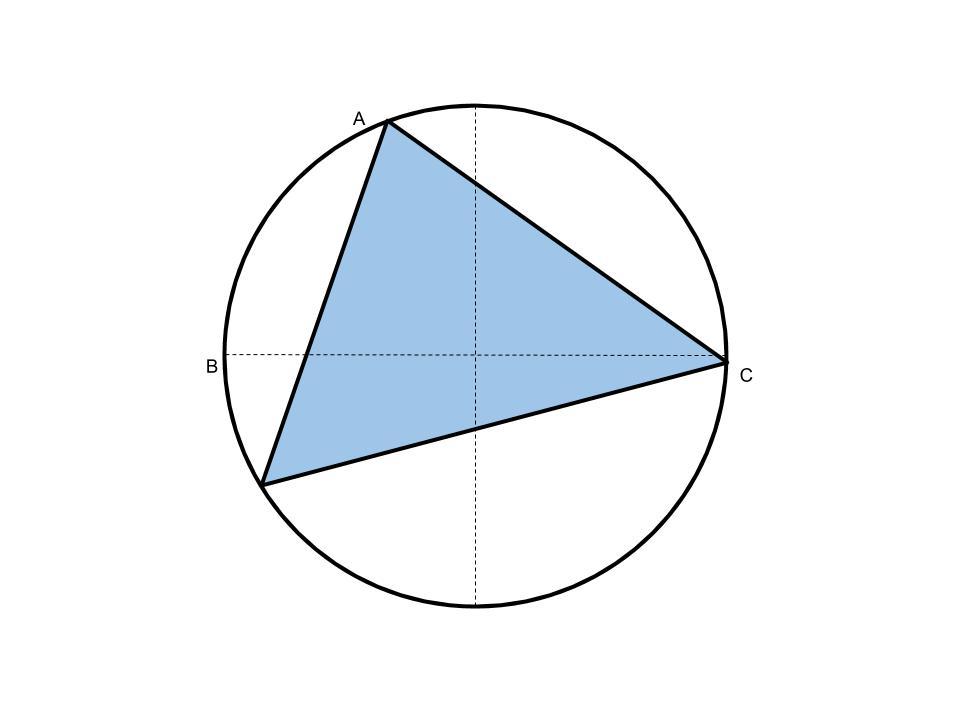
Triangle ABC is stuck in a circle. Its points are on random areas on the circumference of the circle. What is the probability of the triangle covering the centre of the circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This 3Blue1Brown video beautifully explains the answer along with another cool fact
I have watched the video before and posted this problem.
This problem has been posted before. Here's the solution I submitted last time.
Given two points
A
,
B
on a circle, the third point
C
must lie in the red region below if
△
A
B
C
is to contain the circle's center:
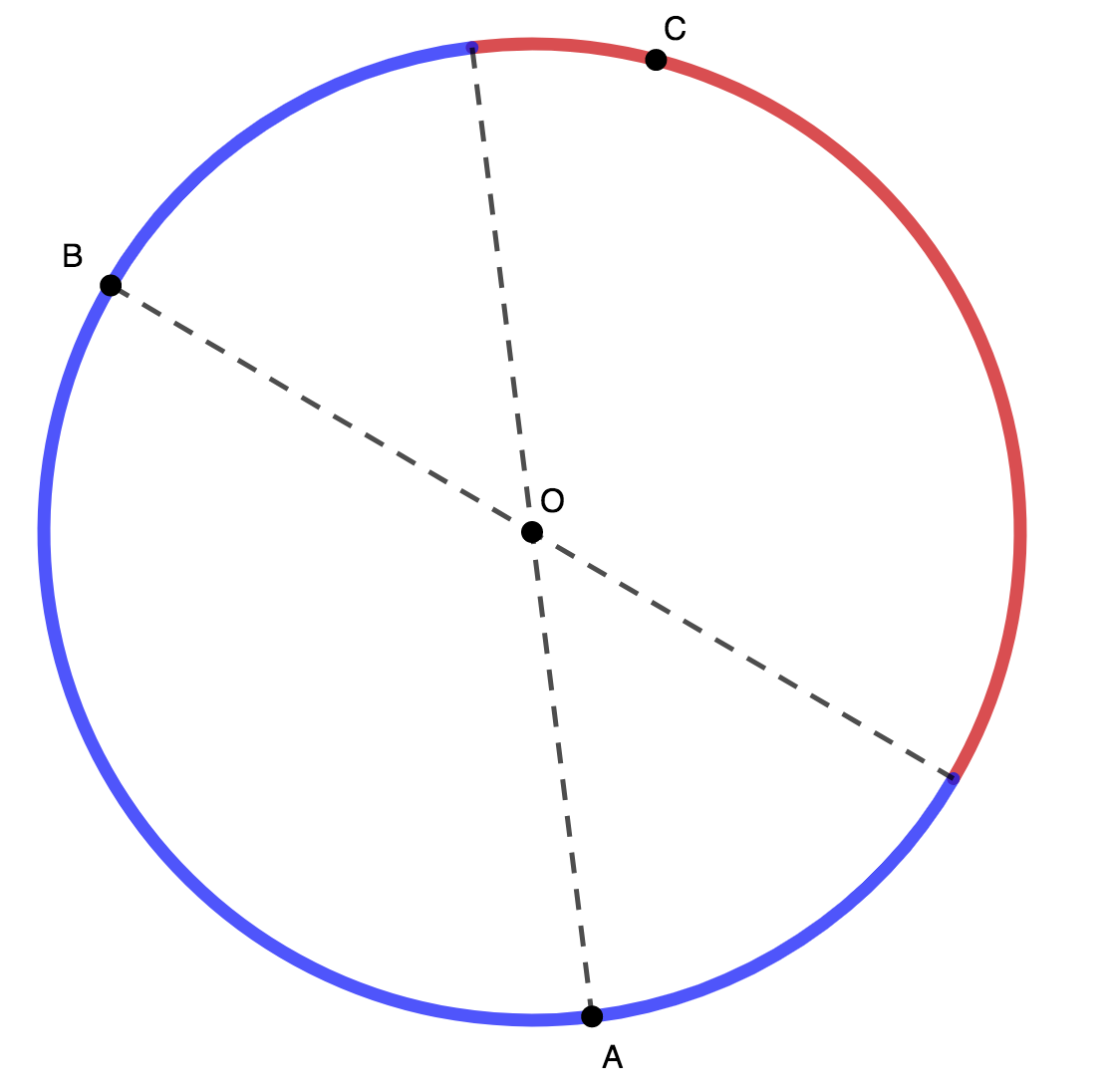
Now, we find the probability of this happening. Fix A and B on the circle, and let θ be the angle between them ( ∠ A O B ). Then 0 < θ ≤ π . Note that the angle intercepting the red region in the diagram is precisely θ . Thus the probability of a random point C being placed in the red area is 2 π θ . We integrate to compute the average probability over all possible θ : π − 0 1 ∫ 0 π 2 π θ d θ = π 1 [ 4 π θ 2 ] θ = 0 π = 4 π 2 π 2 = 4 1 = 2 5 %
I disagree. I think that it is a 50% chance because if you place two points a and b on random places on the circumference of the circle, then it is up to the third point to determine whether or not the triangle covers the center because it has a 50% chance of being on either side of the line starting on a or b that passes through the center.
Log in to reply
Wait, actually that argument was wrong. I think it was actually 25%
By extension of Thales Theorem , if any angle in the triangle is obtuse, the triangle will not contain the center. Therefore, we are looking for the percentage of possible triangles that are not obtuse triangles.
Let A , B , and C be the points on the circle and let O be the center of the circle. Then without loss of generality, the points can be rotated so that A is on the positive x -axis. Then let x be the central angle between A and B and y be the central angle between A and C . Then both x and y are such that 0 ≤ x < 3 6 0 ° and 0 ≤ y < 3 6 0 ° .
△ A O B , △ B O C , and △ A O C are isosceles triangles because each have two sides that are radii of the circle.
If y > x , the base angles of these triangles are 9 0 ° − 2 x , 9 0 ° − 2 y + 2 x , and 9 0 ° − 2 y , which makes ∠ B A C = 2 y − x , ∠ A B C = 1 8 0 ° − 2 y , and ∠ A C B = 2 x . For any one of these angles to be obtuse, either 2 y − x ≥ 9 0 ° or y ≥ x + 1 8 0 ° , 1 8 0 ° − 2 y ≥ 9 0 ° or y ≤ 1 8 0 ° , or 2 x ≥ 9 0 ° or x ≥ 1 8 0 ° , which is shaded in red in the graph below:
By symmetry, if x > y , for any one of these angles to be obtuse, either y ≤ x − 1 8 0 ° , x ≤ 1 8 0 ° , or y ≥ 1 8 0 ° , which is shaded in red in the graph below:
Combining these graphs gives a visual representation of all the possible triangles that can be made by three points on the circumference of a circle, with the red regions showing the triangles that are obtuse, and the green regions showing the triangles that are not obtuse:
The percentage of the green regions represents the probability of a triangle covering the center of the circle, which is 8 2 = 4 1 = 2 5 % .