A triangle and a square in a regular pentagon
Given a regular pentagon (Equal side lengths and interior angles). The line and intersect at the point .
Find
where
denotes the area of
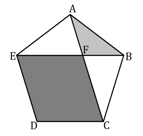
Further Challenges: Assume that you only know the value of . Don't use multiple angle formulas.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
(0) Labeling angles, you'll get
(1) ∠ A E B = ∠ B A C = 3 6 o = 5 π r by the fact that Δ A E B is an isosceles triangle
and
(2) ∠ E A F = ∠ E F A = 7 2 o = 5 2 π r ( ∠ E A F = ∠ E A B − ∠ B A C ) , making Δ A E F an isosceles triangle.
(3) After that, draw A P such that A P is perpendicular to B E and since earlier we get ∠ A E B = 3 6 o = 5 π r , by trigonometry, we get that E P is 4 1 + 5 x . (Let the pentagon's side length equal to x .
(4) By using the fact A P is perpendicular to B E and A E B is an isosceles triangle, B E = 2 A P = 2 1 + 5 .
(5) Because Δ A E F is an isosceles triangle, A E = E F = x .**
(6) Connect C E , this will split C D E F into two identical triangles, Δ E F C and Δ C D E
(7) After labeling more angles, Δ E F C is similar to \(\Delta AFB).
**(8)** From (4) and (5), we can now find \(FB\) which is E B − E F = 2 1 + 5 x − x = 2 5 − 1 x .
(9) If two triangles are similar, the ratio of the area is equal to the ratio of the adjacent side lengths squared, from (7), Δ E F C is similar to Δ A F B and (8), the ratio of the adjacent side lengths (In this case, E F F B ) is x 2 5 − 1 x = 2 5 − 1 , thus it follows that [ Δ C E F [ Δ A F B ] = 2 5 − 1 2 = 2 3 − 5 .
(10) From (6), [ C D E F ] [ Δ E F C ] = 2 1 and italicized claim , it then follows [ Δ C D E F ] [ Δ A F B ] = 2 [ Δ C E F ] [ Δ A F B ] = 4 3 − 5
.
Bonus from the challenge: This method uses cos 3 6 only once!