A triangle made of beams

The triangle ABC is an isosceles triangle. The side AB and AC rotate at angular speed $\omega$ . The length of side BC is constant. The angle A is decreasing at a rate of $\frac{\pi}{4}$ and it will be equal to $2\omega$ because both the sides AB and AC are rotating at $\omega$ to reduce the angle A, that means we have, $2\omega = \frac{\pi}{4}$

Now, consider the half triangle ADC (with D as the right angle) at a certain instant when the side BC is y distance away from the corner A and the angle BAD equals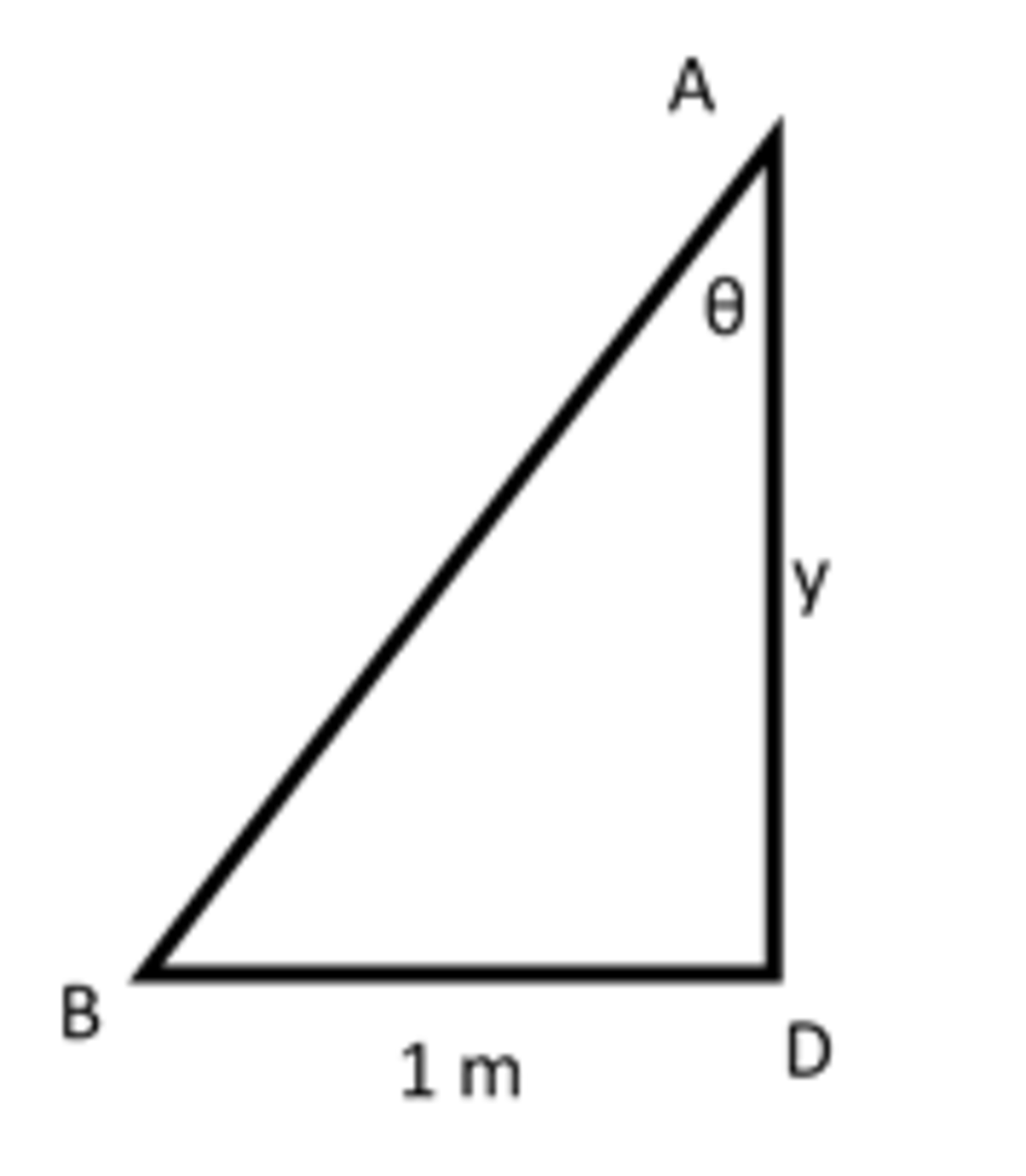 $\theta$

In this triangle,
$tan \theta = \frac{1}{y}$
$y=cot \theta$
Also, we have the speed of the side BC = V = $\frac{dy}{dt}$
Therefore,
$V=\frac{dy}{dt}= - {cosec ^2 \theta} \frac{{d\theta }}{{dt}}$
Here, $\frac{d \theta}{dt} = - \omega$
Hence,
$V= \omega {cosec ^2\theta}$
The instant when the angle BAC becomes right angled then the angle BAD becomes half of it that is $\frac{\pi}{4}$
$V=\omega {cosec^2 \frac{\pi}{4}} = \frac{\pi}{4}$
and $y=cot \frac{\pi}{4} = 1$ .

Once the rod BC is detached it moves on an icy floor with a retardation of $\frac{friction}{mass}$
$friction = \mu mg$ and hence the retardation $a= \mu g$ .
Since the retardation is constant, we can write
${v^2} = {u^2} + 2aS$
Here, v is the final speed that is zero, u is the initial speed that is $\frac{\pi}{4}$ , a is acceleration = $-\mu g$ and S is the displacement.
Therefore, the displacement $S=\frac{V^2}{2\mu g}=3$
and the distance from the corner A will be y+S = 1+3 = 4m.