A triangle of cylinders (part 2)

I am here writing up the equation. The forces acting and accelerations are shown in figure.

$Mg-2Ncos(30)-2fsin(30)=Ma$ ................(1)

$Ncos(60)-fcos(30)=M{ a }_{ 2 }$ ........(2)

$f=\frac { M{ R }^{ 2 } }{ 2 } \alpha$ ................(3)

Let $R\alpha ={ a }_{ 1 }$

Now writing the constraint equations--

Here I have assume that friction is sufficient and the spheres does not slide over each other. They roll over other.

So equation their acceleration in tangential direction we get

${ a }_{ 1 }-{ a }_{ 2 }cos(30)=acos(60)$ ............................(4)

As the sphere are in contact with each other so equating their accelerations in common normal direction we get

${ a }_{ 2 }cos(60)=acos(30)$ ..................(5)

On solving we get $a=g/11$

NOTE- I have found equation (4) using superposition of accelerations about the CoM and of CoM. Here is a figure which makes it clear.

:)

As the cylinders move, suppose that the height of the middle cylinder above the ground is $y$ , and that the horizontal distance of either lower cylinder from the midpoint is $x$ . Suppose also that $\theta$ is the angle indicated in the diagram, and that $\omega$ is the angular speed of one of the lower cylinders, as shown.

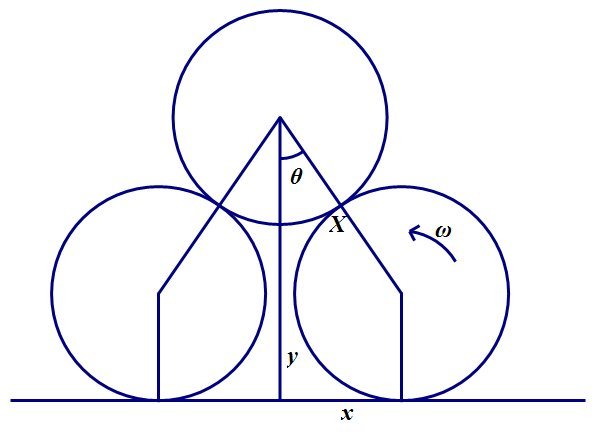
Since there is (presumed to be) no slipping between the upper and lower cylinders the upper cylinder moves vertically downwards with zero angular velocity, and hence the velocity of the point $X$ must have no horizontal component. Thinking about $X$ as a point on the lower cylinder, the velocity of the point $X$ is $(\dot{x},0) + R\omega(-\cos\theta,-\sin\theta) \; = \; (\dot{x} - R\omega \cos\theta, -R\omega \sin\theta) \;,$ Thinking about $X$ as a point on the upper cylinder, the velocity of $X$ is $(0,\dot{y}) \;.$ Thus we deduce that $\dot{x} \,=\, R\omega\cos\theta$ and $\dot{y} \,=\, -R\omega\sin\theta$ . Since geometry tells us that $x \,=\, 2R\sin\theta$ and $y \,=\, 2R\cos\theta + R$ , we deduce that $2\dot\theta \; = \; \omega \;.$ The kinetic energy of the system is $2\times \tfrac12m\dot{x}^2 + 2\times \tfrac12I\omega^2 + \tfrac12m\dot{y}^2 \; = \; m\dot{x}^2 + \tfrac12m\dot{y}^2 + I\omega^2 \; =\; 2mR^2(2 + \cos^2\theta)\dot{\theta}^2 \;,$ where $m$ is the mass of each cylinder, and $I = \tfrac12mR^2$ the moment of inertia of each cylinder about its centre. The gravitational potential energy of the system is $mgy \,=\, mgR(2\cos\theta + 1)$ , we deduce that $2mR^2(2 + \cos^2\theta)\dot{\theta}^2 + mgR(2\cos\theta + 1) \; =\; c \;.$ Differentiating this identity with respect to time, and cancelling a factor of $\dot{\theta}$ , gives $4mR^2(2 + \cos^2\theta)\ddot{\theta} - 4mR^2\sin\theta\cos\theta \dot{\theta}^2 - 2mgR\sin\theta \; = \; 0 \;.$ When $t=0$ we have $\theta = \tfrac16\pi$ , $\dot\theta=0$ , and hence $\ddot{\theta} = \tfrac{g}{11R}$ .

Since $\dot{y} \,=\, -2R\sin\theta \dot{\theta}$ , we have $\ddot{y} \,=\, -2R\cos\theta \dot{\theta}^2 - 2R\sin\theta \ddot{\theta}$ , and hence the initial value of $\ddot{y}$ is $-\tfrac{1}{11}g \,=\, -\tfrac{10}{11}$ , making the answer $10+11 = \boxed{21}$ .