A triangle surrounded by circles
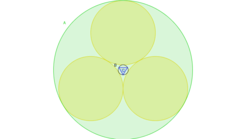 In a circle
A
with radius
6
1
8
+
4
3
2
we draw
3
circles with equal radii, in such way that each of them are tangent to the other
2
circles and to circle
A
. Inside the circle
A
we draw a circle
B
in such way that is tangent to each of the
3
new circles. An equilateral triangle
C
is inscribed in
B
.
In a circle
A
with radius
6
1
8
+
4
3
2
we draw
3
circles with equal radii, in such way that each of them are tangent to the other
2
circles and to circle
A
. Inside the circle
A
we draw a circle
B
in such way that is tangent to each of the
3
new circles. An equilateral triangle
C
is inscribed in
B
.
If the area of C can be written in the form:
d a b − c
Where a , b , c and d are integers such that b ∣ a and d ∣ c .
Find:
a + b + c + d
The answer is 178.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Sea R el radio del círculo A , r el radio del círculo B y b el radio de los tres círculos pequeños. Usemos el teorema de círculos de Descartes. Nos dice que:
( a 1 + b 3 ) 2 = 2 ( a 2 1 + b 2 3 )
Donde a puede ser − R o r , también según el teorema de Descartes. Expandimos y simplificamos:
3 a 2 + 6 a b − b 2 = 0
Sabemos que una raíz de esa ecuación es − R = − ( 3 + 2 3 ) y queremos encontrar r . Por las fórmulas de Vieta sabemos que:
− R + r = − 2 b ⟹ 3 + 2 3 − r = 2 b − R r = − 3 b 2 ⟹ r ( 3 + 2 3 ) = 3 b 2
Resolviendo ese sistema en los números positivos obtenemos b = 3 y r = 2 3 − 3 .
Por último, el área de un triángulo equilátero C inscrito en un círculo de radio r es:
A C = 4 3 3 r 2 = 4 3 3 ( 2 3 − 3 ) 2 = 4 6 3 3 − 1 0 8
Finalmente, a = 6 3 , b = 3 , c = 1 0 8 , d = 4 y a + b + c + d = 1 7 8 .
Tambien use el teorema de Descartes, me gusto como usaste las fórmulas de Vieta, creo que eso simplifico el problema porque se encuentran los 2 radios de una vez en lugar de usar 2 veces el teorema de Descartes.
We solve this problem using Descartes' circle theorem. Let the radii of the 3 equal circles be r0 and the large one be r1. Define k0=1/r0 and k1=1/k1.
The theorem says that 3k0^2-k1^2+6k0k1=0. Since we know what k3 is, we can solve for k3. Note that negative solutions are possible. Simply take the modulus in this case. This is due to the fact that k1,k0 are curvatures and curvatures can be negative.
Since the radius of the larger circle is bigger than that of the smaller one, k1<k0. We can discard one of the solutions this way.
Then, use this value of k0 to solve for the 2 values of k3. One of the values will correspond to the radius of the larger circle. The other will correspond to the radius of the smaller circle. This gives us r=2sqrt(3)-3.
Now using the extended sine rule, we see that s/sin(60) = 2r where s is the side length of the triangle. This gives us s=6-3sqrt(3).
Now we use the well known formula that the area of a triangle is s^2sqrt(3)/2 to find that the answer is (63sqrt(3)-108)/4 . We note that the values of the numbers satisfy the conditions needed so a+b+c+d= 63+3 +108+4=178.
NOTE: Descartes' theorem is a theorem often used in circle inversion problems which are very interesting and often come up in Olympiad questions.
Since Replay is not working in Chew-Seong Cheong solution, I am writing here. I used the same approach, arriving at some values through different path.
Area of an equilateral triangle in terms of circumradius r, A = 4 3 ∗ 3 ∗ r 2 In an equilateral triangle circumradius r in terms of side S is, r = 3 S And Sum of radii of the small and an equal circle is the circunradius of e q u i l a t e r a l Δ P Q R .
It is given that the radius of circle A ,
r A = 6 1 8 + 4 3 2 = 6 1 8 + 1 2 3 = 3 + 2 3 .
Now let the center of circle A be O , and the centers and radius of the three smaller circle be P , Q and R , and r . Then △ P Q R is an equilateral triangle with sides 2 r . We note that O P , O Q and O R are along the diameters of the small circles connecting the three tangent points to O . Therefore, we know that:
r A = r + O P = r + cos 3 0 ∘ r = ( 1 + 3 2 ) r
= ( 1 + 3 2 3 ) r = 3 ( 3 + 2 3 ) r
⇒ r = 3 + 2 3 3 r A = 3 + 2 3 3 × ( 3 + 2 3 ) = 3
We also note that radius r B of circle B is given by:
r B = cos 3 0 ∘ r − r = ( 3 2 − 1 ) r = 3 ( 2 3 − 3 ) r
= 3 ( 2 3 − 3 ) ( 3 ) = 2 3 − 3
The area of △ C is equal to 3 × that of r B -side isosceles triangle.
A C = 3 × 2 1 × 2 r B cos 3 0 ∘ × r B sin 3 0 ∘ = 4 3 3 r B 2
= 4 3 3 ( 2 3 − 3 ) 2 = 4 3 3 ( 1 2 − 1 2 3 + 9 )
= 4 3 3 ( 2 1 − 1 2 3 ) = 4 6 3 3 − 1 0 8
⇒ a = 6 3 , b = 3 , c = 1 0 8 , d = 4 and a + b + c + d = 1 7 8