A triangular geometry problem: 2
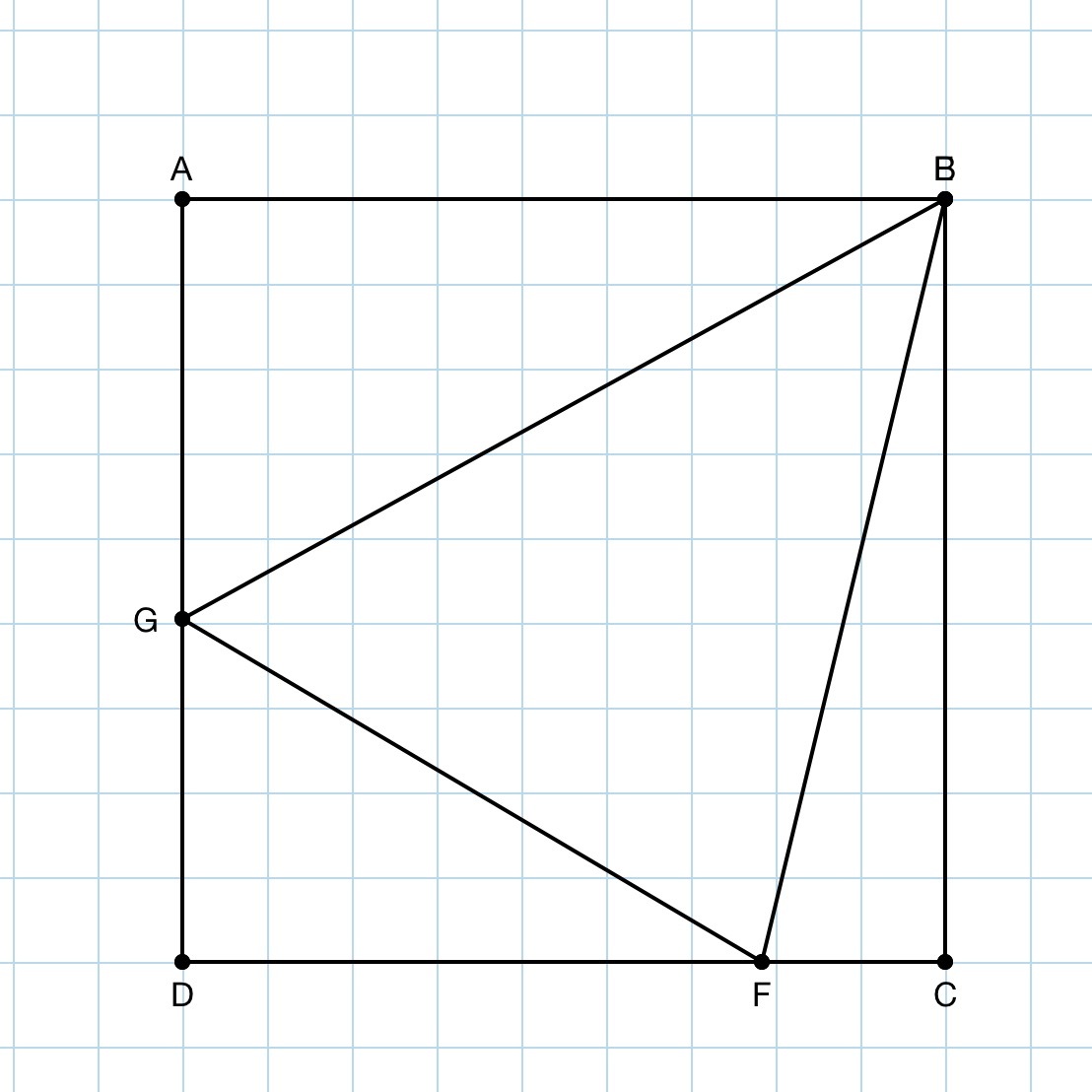 As shown in the image, a triangle BFG, is inscribed in the square ABCD. Given that the triangle GFD has a perimeter of 2cm, and the square has sides 1cm, find angle GBF to its exact value in degrees.
Note that the diagram is not to scale!
As shown in the image, a triangle BFG, is inscribed in the square ABCD. Given that the triangle GFD has a perimeter of 2cm, and the square has sides 1cm, find angle GBF to its exact value in degrees.
Note that the diagram is not to scale!
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
let ∠ A B G = t and ∠ C B F = s , then the perimeter condition on △ G F D implies that
2 = ( 1 − tan t ) + ( 1 − tan s ) + sec 2 t + sec 2 s − 2 sec t sec s cos ( 2 π − ( t + s ) )
Therefore,
0 = − tan t − tan s + sec 2 t + sec 2 s − 2 sec t sec s sin ( t + s )
Multiplying through by cos t cos s results in,
0 = − sin t cos s − cos t sin s + cos 2 s + cos 2 t − 2 cos s cos t sin ( t + s )
Hence,
( sin t cos s + cos t sin s ) 2 = cos 2 s + cos 2 t − 2 cos s cos t sin ( t + s )
Expanding the left hand side,
sin 2 t cos 2 s + cos 2 t sin 2 s + 2 sin t sin s cos t cos s = cos 2 s + cos 2 t − 2 cos s cos t sin ( t + s )
Collecting terms,
c o s 2 s ( s i n 2 s − 1 ) + cos 2 t ( sin 2 s − 1 ) + 2 sin t sin s cos t cos s = − 2 cos s cos t sin ( t + s )
Hence,
− 2 cos 2 s cos 2 t + 2 sin t sin s cos t cos s = − 2 cos s cos t sin ( t + s )
Dividing through by − 2 cos s cos t ,
cos s cos t − sin t sin s = sin ( t + s )
Therefore,
cos ( t + s ) = sin ( t + s )
Which implies
tan ( t + s ) = 1 , so that ( t + s ) = 4 5 ∘
Finally, ∠ G B F = 9 0 ∘ − ( t + s ) = 9 0 ∘ − 4 5 ∘ = 4 5 ∘
Let ∣ D F ∣ = x and ∣ D G ∣ = y . Then we require that x + y + x 2 + y 2 = 2 , and so
x 2 + y 2 = 2 − ( x + y ) ⟹ x 2 + y 2 = 4 + ( x + y ) 2 − 4 ( x + y ) = 4 + x 2 + y 2 + 2 x y − 4 x − 4 y ⟹ 4 y − 2 x y = 4 − 4 x ⟹ y = 2 − x 2 ( 1 − x ) .
Now ∠ G B F = 2 π − ∠ F B C − ∠ A B G = 2 π − arctan ( 1 − x ) − arctan ( 1 − y ) =
2 π − ( arctan ( 1 − x ) + arctan ( 1 − 2 − x 2 ( 1 − x ) ) ) = 2 π − ( arctan ( 1 − x ) + arctan ( 2 − x x ) ) .
Next, using the arctan addition formula arctan ( u ) + arctan ( v ) = arctan ( 1 − u v u + v ) we find that
arctan ( 1 − x ) + arctan ( 2 − x x ) = arctan ⎝ ⎜ ⎜ ⎛ 1 − 2 − x x ( 1 − x ) 1 − x + 2 − x x ⎠ ⎟ ⎟ ⎞ = arctan ( 2 − x − x ( 1 − x ) ( 1 − x ) ( 2 − x ) + x ) = arctan ( 2 − 2 x + x 2 2 − 2 x + x 2 ) = arctan ( 1 ) = 4 π .
So finally ∠ G B F = 2 π − 4 π = 4 π = 4 5 ∘ .
Let AG=a, and FC=b.By using Pythagoras GF=((1-a)^2 +(1-b)^2)^0.5. The perimeter : (1-a)+(1-b) +((1-a)^2 +(1-b)^2)^0.5 =2, We get (a+b)^2 = (1-a)^2 +(1-b)^2, or b=(1-a)/(1+a). Tan (ABG + FBC) = [a + (1-a)/(1+a)]/[1- a * (1-a)/(1+a)] =[a^2+1]/[a^2+1]=1. So the angle of (ABG + FBC) = 45.Finally the angle GBF = 90- 45 = 45
Thanks to all for writing a solution! I am actually surprised to see a such detailed and complex solution, as I did this problem in a very different way: 1. Take the lengths GD and DF as length a and b respectively. 2. We deduce that GF is 2-a-b 3.imagine rotating triangle BAG by 90 degrees anti clockwise, forming a new triangle BFG'. 4. FC is 1-b, and CG' is 1-a, hence FG' is equal to FG, deducing that BFG and BFG' is actually congruent. 5.angle GBG' is 90 degrees and bisected by angle GBF, so GBF=90/2=45.