A Tricky Visual Calculus Problem

Calculus Level 2

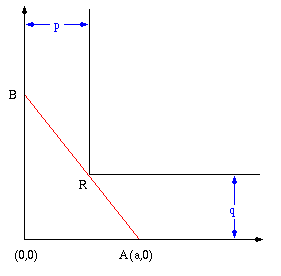What is the approximate length of the longest ladder (in feet) you can carry horizontally around the corner of the corridor shown here?

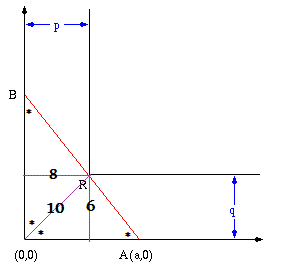
A B AB is the ladder and the coordinate of R R is ( 8 , 6 ) (8,6) .


The answer is 19.731.

View wiki
Venkatesh K by Venkatesh K , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Let θ = ∠ O A B , \theta = \angle OAB, where O ( 0 , 0 ) O(0,0) is the origin. (Note that we are looking for 0 < θ < π 2 . 0 \lt \theta \lt \frac{\pi}{2}. ) Then the length of the ladder is

L = ∣ A R ∣ + ∣ R B ∣ = 6 sin ⁡ ( θ ) + 8 cos ⁡ ( θ ) , L = |AR| + |RB| = \dfrac{6}{\sin(\theta)} + \dfrac{8}{\cos(\theta)}, (A).

Now differentiate with respect to θ \theta and set equal to 0 : 0:

d L d θ = 6 cos ⁡ ( θ ) sin ⁡ 2 ( θ ) − 8 sin ⁡ ( θ ) cos ⁡ 2 ( θ ) = 6 cos ⁡ 3 ( θ ) − 8 sin ⁡ 3 ( θ ) sin ⁡ 2 ( θ ) cos ⁡ 2 ( θ ) = 0 \dfrac{dL}{d\theta} = \dfrac{6\cos(\theta)}{\sin^{2}(\theta)} - \dfrac{8\sin(\theta)}{\cos^{2}(\theta)} = \dfrac{6\cos^{3}(\theta) - 8\sin^{3}(\theta)}{\sin^{2}(\theta)\cos^{2}(\theta)} = 0

when 6 cos ⁡ 3 ( θ ) = 8 sin ⁡ 3 ( θ ) ⟹ tan ⁡ ( θ ) = 3 4 3 6\cos^{3}(\theta) = 8\sin^{3}(\theta) \Longrightarrow \tan(\theta) = \sqrt[3]{\dfrac{3}{4}}

⟹ θ = 0.737524472.... \Longrightarrow \theta = 0.737524472.... radians.

Now L → ∞ L \rightarrow \infty as θ → 0 \theta \rightarrow 0 and θ → π 2 , \theta \rightarrow \frac{\pi}{2}, so the critical point obtained must yield a minimum, which in turn corresponds to the longest possible ladder that can be carried around the corner of the corridor. Plugging the value for θ \theta found above into equation (A), we find that the desired length of the ladder is

L = 19.731 L = \boxed{19.731} feet to 3 decimal places.

17 Helpful 0 Interesting 0 Brilliant 0 Confused

sir , i have written a solution for this problem, tell me ,it is correct or not.

manish kumar singh - 5 years, 7 months ago

Brian sir, I have a doubt. The longest ladder can be of infinite length. The question should ask the length of shortest ladder. Am I wrong anywhere? Please correct me.

Rinkon Saha - 5 years, 1 month ago

for the length of the ladder to be maximum ,the ladder must pass through R(8,6). let A has coordinate (a,0) and B has coordinate (0,b). then eqn of straight line AB is x/a +x/b =1. this st. line passes through point R, HENCE we have, 8/a + 6/b =1. which gives b=(6 a)/(a - 8). now length of ladder is given by, L= sqrt(a^2 + b^2). PUT b in terms of a, we have L^2= a^2 +[ 36 a^2/(a-8)^2]. for length to be maximum d(L)/d (a) =0. which gives a =14.6038, and b= 13.2686. so longest length = sqrt(a^2+b^2)= 19.7313 (approx).

2 Helpful 0 Interesting 0 Brilliant 0 Confused

This is a great approach, but I think that you may have made a mistake after setting d L d a = 0 , \dfrac{dL}{da} = 0, since I'm getting different values for a a and b . b. Rewriting your equation for L 2 L^{2} as

L 2 = a 2 ( 1 + 36 ( a − 8 ) 2 ) L^{2} = a^{2}\left(1 + \dfrac{36}{(a - 8)^{2}}\right)

and then differentiating with respect to a a using the product rule, we find that

2 L d L d a = 2 a ( 1 + 36 ( a − 8 ) 2 ) + a 2 ( − 2 ∗ 36 ( a − 8 ) 3 ) 2L\dfrac{dL}{da} = 2a\left(1 + \dfrac{36}{(a - 8)^{2}}\right) + a^{2}\left(\dfrac{-2*36}{(a - 8)^{3}}\right)

⟹ d L d a = a L ( 1 + 36 ( a − 8 ) 2 − 36 a ( a − 8 ) 3 ) = \Longrightarrow \dfrac{dL}{da} = \dfrac{a}{L}\left(1 + \dfrac{36}{(a - 8)^{2}} - \dfrac{36a}{(a - 8)^{3}}\right) =

a L ( 1 + 36 ( a − 8 ) 2 ( 1 − a ( a − 8 ) ) ) = a L ( 1 − 36 ∗ 8 ( a − 8 ) 3 ) . \dfrac{a}{L}\left(1 + \dfrac{36}{(a - 8)^{2}}\left(1 - \dfrac{a}{(a - 8)}\right)\right) = \dfrac{a}{L}\left(1 - \dfrac{36*8}{(a - 8)^{3}}\right).

Then since a , L > 0 a,L \gt 0 we see that d L d a = 0 \dfrac{dL}{da} = 0 when

1 = 36 ∗ 8 ( a − 8 ) 3 ⟹ a − 8 = ( 8 ∗ 36 ) 1 3 = 2 ∗ 6 2 3 ⟹ a = 8 + 2 ∗ 6 2 3 = 14.604 1 = \dfrac{36*8}{(a - 8)^{3}} \Longrightarrow a - 8 = (8*36)^{\frac{1}{3}} = 2*6^{\frac{2}{3}} \Longrightarrow a = 8 + 2*6^{\frac{2}{3}} = 14.604

to 3 decimal places, in which case b = 6 a a − 8 = 13.268 b = \dfrac{6a}{a - 8} = 13.268 to 3 decimal places, and so L = 14.60 4 2 + 13.26 8 2 = 19.731 L = \sqrt{14.604^{2} + 13.268^{2}} = 19.731 to 3 decimal places, in agreement with my solution. Otherwise, good work. :)

(There are also a couple of typos, but these don't affect your equation for L 2 . L^{2}. The coordinates for B B should be ( 0 , b ) , (0,b), and the equation for the line A B AB should be x / a + y / b = 1. x/a + y/b = 1. )

Brian Charlesworth - 5 years, 7 months ago

Log in to reply

sorry sir, yes B is (0,b). i also differentiated L^2 with respect to 'a'. actually i am not good at Latex, so i directly wrote values after calculating on paper, and you are right ,i have done wrong calculation . a= 14.6038 and b= 13.268, so L =19.731.i have edited. Thank you.

manish kumar singh - 5 years, 7 months ago
Care No More
Aug 28, 2015

simple,imprecise solution "20"

2 Helpful 0 Interesting 0 Brilliant 0 Confused

i think u said it using the property of circumvented.but u can't tell that's the centre

Ridhu Paran - 5 years, 1 month ago

I did it in a similar way but it's not correct to consider OR = RA

Apoorva Singal - 11 months, 3 weeks ago
Sourabh Jain
Aug 16, 2015

just scale that and prove it approx value is 20 :P

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Hadia Qadir
Aug 12, 2015

The approximate length of the longest ladder (infeet) one can carry horizontally around the corner of the corridor shown is [8^(2/3 + 6^2/3]^3/2 = 19.731 ft.

1 Helpful 0 Interesting 0 Brilliant 1 Confused 
1
2
3
 
answer**(2/3) = 8**(2/3) + 6**(2/3)

answer = 19.7313

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...